
(本題12分)某公司是專門生產健身產品的企業,第一批產品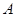 上市銷售40天內全部售完,該公司對第一批產品
上市銷售40天內全部售完,該公司對第一批產品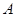 上市后的市場銷售進行調研,結果如圖(1)、(2)所示.其中(1)的拋物線表示的是市場的日銷售量與上市時間的關系;(2)的折線表示的是每件產品
上市后的市場銷售進行調研,結果如圖(1)、(2)所示.其中(1)的拋物線表示的是市場的日銷售量與上市時間的關系;(2)的折線表示的是每件產品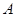 的銷售利潤與上市時間的關系.
的銷售利潤與上市時間的關系.
(1)寫出市場的日銷售量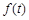 與第一批產品A上市時間t的關系式;
與第一批產品A上市時間t的關系式;
(2)第一批產品A上市后的第幾天,這家公司日銷售利潤最大,最大利潤是多少?
(1)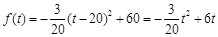
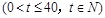 ;
;
(2)第一批產品A上市后的第27天這家公司日銷售利潤最大,最大利潤是 萬元.
萬元.
解析試題分析:(1)先根據題意設f(t)=a(t-20)2+60,由f(0)=0求得a值即得日銷售量f(t)(2)與第一批產品A上市時間t的關系式;
(2)先寫出銷售利潤為g(t)萬元,分類討論:當30≤t≤40時,當0<t≤30時,分別研究它們的單調性,而t∈N,故比較g(26),g(27)即可,經計算,g(26)<g(27),故第一批產品A上市后的第27天這家公司日銷售利潤最大。
解:(1) 設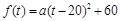 ,由
,由 可知
可知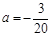
即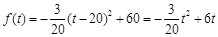
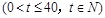 ;……………4分
;……………4分
(2) 設銷售利潤為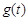 萬元,則
萬元,則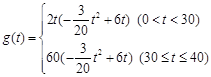 ……………………8分
……………………8分
當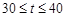 時,
時,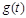 單調遞減;
單調遞減;
當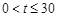 時,
時,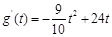 ,易知
,易知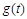 在
在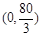 單增,
單增,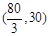 單減,而
單減,而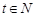 ,故比較
,故比較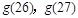 ,經計算,
,經計算,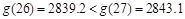 ,故第一批產品A上市后的第27天這家公司日銷售利潤最大,最大利潤是
,故第一批產品A上市后的第27天這家公司日銷售利潤最大,最大利潤是 萬元.………………12分
萬元.………………12分
考點:本試題主要考查了分段函數,以及函數與方程的思想,屬于基礎題.
點評:解決該試題的函數模型為分段函數,求分段函數的最值,應先求出函數在各部分的最值,然后取各部分的最值的最大值為整個函數的最大值,取各部分的最小者為整個函數的最小值.


科目:高中數學 來源: 題型:解答題
(本小題共12分)已知f(x)=m(x-2m)(x+m+3),g(x)=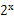 -2,若同時滿足條件:
-2,若同時滿足條件:
①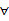 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②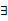 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范圍。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=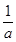 -
-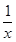 (a>0,x>0).
(a>0,x>0).
(1)用函數的單調性定義證明:f(x)在(0,+∞)上是增函數;
(2)若f(x)在[ ,2]上的值域是[
,2]上的值域是[ ,2],求實數a的值.
,2],求實數a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com