
【題目】如圖,邊長為2的等邊△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,M為BC的中點(diǎn).
,M為BC的中點(diǎn).
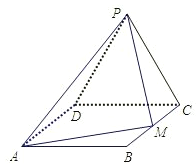
(I)證明:AM⊥PM ;
(II)求二面角P-AM-D的大小.
【答案】(1)見解析; (2)45°.
【解析】
(Ⅰ)以D點(diǎn)為原點(diǎn),分別以直線DA、DC為x軸、y軸,建立如圖所示的空間直角坐標(biāo)系![]() ,求出
,求出![]() 與
與![]() 的坐標(biāo),利用數(shù)量積為零,即可證得結(jié)果;(Ⅱ)求出平面PAM與平面ABCD的法向量,代入公式即可得到結(jié)果.
的坐標(biāo),利用數(shù)量積為零,即可證得結(jié)果;(Ⅱ)求出平面PAM與平面ABCD的法向量,代入公式即可得到結(jié)果.
(I)證明:以D點(diǎn)為原點(diǎn),分別以直線DA、DC為x軸、y軸,建立如圖所示的空間直角坐標(biāo)系![]() ,依題意,可得
,依題意,可得![]()
![]()
∴![]()
![]()
∴![]()
即![]() ,∴AM⊥PM .
,∴AM⊥PM .
(II)設(shè)![]() ,且
,且![]() 平面PAM,則
平面PAM,則
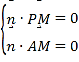 ,即
,即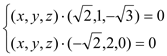 ∴
∴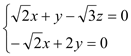 ,
,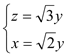
取![]() ,得
,得![]() ;取
;取![]() ,顯然
,顯然![]() 平面ABCD,
平面ABCD,
∴![]() ,結(jié)合圖形可知,二面角P-AM-D為45°.
,結(jié)合圖形可知,二面角P-AM-D為45°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有限集S中的元素個數(shù)記作![]() ,設(shè)A、B是有限集合,給出下列命題:
,設(shè)A、B是有限集合,給出下列命題:
(1)![]() 的充分不必要條件是
的充分不必要條件是![]() ;
;
(2)![]() 的必要不充分條件是
的必要不充分條件是![]() ;
;
(3)![]() 的充要條件是
的充要條件是![]()
其中假命題是(寫題號)________________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國家邊防安全條例規(guī)定:當(dāng)外輪與我國海岸線的距離小于或等于![]() 海里時,就會被警告.如圖,設(shè)
海里時,就會被警告.如圖,設(shè)![]() ,
,![]() 是海岸線上距離
是海岸線上距離![]() 海里的兩個觀察站,滿足
海里的兩個觀察站,滿足![]() ,一艘外輪在
,一艘外輪在![]() 點(diǎn)滿足
點(diǎn)滿足![]() ,
,![]() .
.

(1)![]() ,
,![]() 滿足什么關(guān)系時,就該向外輪發(fā)出警告令其退出我國海域?
滿足什么關(guān)系時,就該向外輪發(fā)出警告令其退出我國海域?
(2)當(dāng)![]() 時,間
時,間![]() 處于什么范圍內(nèi)可以避免使外輪進(jìn)入被警告區(qū)域?
處于什么范圍內(nèi)可以避免使外輪進(jìn)入被警告區(qū)域?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高校在2012年的自主招生考試成績中隨機(jī)抽取![]() 名中學(xué)生的筆試成績,按成績分組,得到的頻率分布表如表所示.
名中學(xué)生的筆試成績,按成績分組,得到的頻率分布表如表所示.
組號 | 分組 | 頻數(shù) | 頻率 |
第1組 |
| 5 |
|
第2組 |
| ① |
|
第3組 |
| 30 | ② |
第4組 |
| 20 |
|
第5組 |
| 10 |
|

(1)請先求出頻率分布表中![]() 位置的相應(yīng)數(shù)據(jù),再完成頻率分布直方圖;
位置的相應(yīng)數(shù)據(jù),再完成頻率分布直方圖;
(2)為了能選拔出最優(yōu)秀的學(xué)生,高校決定在筆試成績高的第![]() 組中用分層抽樣抽取名學(xué)生進(jìn)入第二輪面試,求第3、4、5組每組各抽取多少名學(xué)生進(jìn)入第二輪面試;
組中用分層抽樣抽取名學(xué)生進(jìn)入第二輪面試,求第3、4、5組每組各抽取多少名學(xué)生進(jìn)入第二輪面試;
(3)在(2)的前提下,學(xué)校決定在![]() 名學(xué)生中隨機(jī)抽取
名學(xué)生中隨機(jī)抽取![]() 名學(xué)生接受
名學(xué)生接受![]() 考官進(jìn)行面試,求:第
考官進(jìn)行面試,求:第![]() 組至少有一名學(xué)生被考官
組至少有一名學(xué)生被考官![]() 面試的概率.
面試的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,過橢圓
中,過橢圓![]() 右頂點(diǎn)
右頂點(diǎn)![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于另外一點(diǎn)
于另外一點(diǎn)![]() ,已知點(diǎn)
,已知點(diǎn)![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn)
兩點(diǎn)![]() 分別在直線
分別在直線![]() 的上、下方,設(shè)四邊形
的上、下方,設(shè)四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,滿足
,滿足![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求證:數(shù)列![]() 是等差數(shù)列,求數(shù)列
是等差數(shù)列,求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com