Question

【題目】已知橢圓C： 的左、右焦點為F1，F2，設點F1，F2與橢圓短軸的一個端點構成斜邊長為4的直角三角形.

(1)求橢圓C的標準方程；

(2)設A，B，P為橢圓C上三點，滿足，記線段AB中點Q的軌跡為E，若直線l：y＝x＋1與軌跡E交于M，N兩點，求|MN|.

Answer 1

【答案】(1) ；(2) .

【解析】試題分析：

（1）由題意可得，即可求出，即可求出橢圓的標準方程；

（2）方法一：設，利用向量，求得點的坐標，根據點在橢圓上，把直線的方程和橢圓方程，利用根與系數的關系、韋達定理，利用弦長公式，即可求解；

方法二：設，根據題意和點在橢圓上，化簡整理可得，再根據中點坐標公式，消去 線段的中點的軌跡方程，再設兩點點坐標為，根據弦長公式即可求出.

試題解析：

(1)由已知得2c＝4，b＝2，故c＝2，a＝2.

故橢圓C的標準方程為＋＝1.

(2)法一　設A(x1，y1)，B(x2，y2)，∵＝＋，∴＝，故點P坐標為.

由于點P在橢圓C上，

故有＋＝1，

＋＋＝1，

即＋＋＝1，即＋＝0.

令線段AB的中點坐標為Q(x，y)，則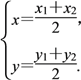

因A，B在橢圓C上，故有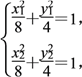

相加有＋＝2.

故＋＝2，

由于＋＝0，

故＋＝2，即Q點的軌跡E的方程為＋＝1.

聯立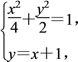得3x2＋4x－2＝0.

設M(x3，y3)，N(x4，y4)，

則x3＋x4＝－，

x3·x4＝－.

故|MN|＝|x3－x4|＝＝.

法二　設A(2cos α，2sin α)，B(2cos β，2sin β)，

∵＝＋，

∴＝，故點P坐標為.

∵點P在橢圓上，

∴(3cos α＋4cos β)2＋(3sin α＋4sin β)2＝25，

∴cos αcos β＋sin αsin β＝0，∴cos(α－β)＝0，

∴α－β＝，

∴B(2sin α，－2cos α)，

∴AB中點Q的坐標為(cos α＋sin α，sin α－cos α)，

設Q的點坐標為(x，y)，

∴x＝cos α＋sin α，y＝sin α－cos α，

∴＝cos2α＋2cos αsin α＋sin2α＝1＋2cos αsin α，

y2＝cos2α－2cos αsin α＋sin2α＝1－2cos αsin α，

∴＋y2＝2，

即線段AB中點Q的軌跡為E的方程為＋＝1.

設M，N兩點的坐標為(x1，y1)，(x2，y2)，

由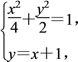消y，

整理得3x2＋4x－2＝0，

∴x1＋x2＝－，x1x2＝－，

∴|MN|＝|x1－x2|＝×＝.