
【題目】某學(xué)校為了解學(xué)生假期參與志愿服務(wù)活動的情況,隨機調(diào)查了![]() 名男生,
名男生,![]() 名女生,得到他們一周參與志愿服務(wù)活動時間的統(tǒng)計數(shù)據(jù)如右表(單位:人):
名女生,得到他們一周參與志愿服務(wù)活動時間的統(tǒng)計數(shù)據(jù)如右表(單位:人):
超過 | 不超過 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握認(rèn)為該校學(xué)生一周參與志愿服務(wù)活動時間是否超過
的把握認(rèn)為該校學(xué)生一周參與志愿服務(wù)活動時間是否超過![]() 小時與性別有關(guān)?
小時與性別有關(guān)?
(2)以這![]() 名學(xué)生參與志愿服務(wù)活動時間超過
名學(xué)生參與志愿服務(wù)活動時間超過![]() 小時的頻率作為該事件發(fā)生的概率,現(xiàn)從該校學(xué)生中隨機抽查
小時的頻率作為該事件發(fā)生的概率,現(xiàn)從該校學(xué)生中隨機抽查![]() 名學(xué)生,試估計這
名學(xué)生,試估計這![]() 名學(xué)生中一周參與志愿服務(wù)活動時間超過
名學(xué)生中一周參與志愿服務(wù)活動時間超過![]() 小時的人數(shù).
小時的人數(shù).
附:
|
|
|
|
|
|
|
|
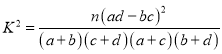
【答案】(1)有,理由見解析;(2)![]() .
.
【解析】
(1)列出![]() 列聯(lián)表,根據(jù)表格中的數(shù)據(jù)計算出
列聯(lián)表,根據(jù)表格中的數(shù)據(jù)計算出![]() 的觀測值,并將
的觀測值,并將![]() 的值與
的值與![]() 作大小比較,即可判斷出題中結(jié)論的正誤;
作大小比較,即可判斷出題中結(jié)論的正誤;
(2)根據(jù)表格中的數(shù)據(jù)得出參與志愿服務(wù)活動時間超過![]() 小時的頻率,然后乘以
小時的頻率,然后乘以![]() 即可得出結(jié)果.
即可得出結(jié)果.
(1)![]() 列聯(lián)表如下表所示:
列聯(lián)表如下表所示:
超過 | 不超過 | 合計 | |
男 |
|
|
|
女 |
|
|
|
合計 |
|
|
|
![]() ,
,
因此,有![]() 的把握認(rèn)為該校學(xué)生一周參與志愿服務(wù)活動時間是否超過
的把握認(rèn)為該校學(xué)生一周參與志愿服務(wù)活動時間是否超過![]() 小時與性別有關(guān);
小時與性別有關(guān);
(2)由表格中的數(shù)據(jù)可知,該校參與志愿服務(wù)活動時間超過![]() 小時的學(xué)生頻率為
小時的學(xué)生頻率為![]() ,
,
因此,抽取的![]() 名學(xué)生中一周參與志愿服務(wù)活動時間超過
名學(xué)生中一周參與志愿服務(wù)活動時間超過![]() 小時的人數(shù)為
小時的人數(shù)為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)雙曲線![]()
![]() 的左右焦點分別為
的左右焦點分別為![]() ,過
,過![]() 的直線分別交雙曲線左右兩支于點M,N.若以MN為直徑的圓經(jīng)過點
的直線分別交雙曲線左右兩支于點M,N.若以MN為直徑的圓經(jīng)過點![]() 且
且![]() ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
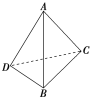
【題目】如圖,在三棱錐A-BCD中,AD⊥BD,AC⊥BC,∠DAB=![]() ,∠BAC=
,∠BAC=![]() .三棱錐的外接球的表面積為16π,則該三棱錐的體積的最大值為( )
.三棱錐的外接球的表面積為16π,則該三棱錐的體積的最大值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
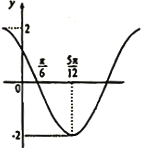
【題目】若函數(shù)![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)![]() ,
,![]() 的部分圖象如圖所示,
的部分圖象如圖所示,![]() ,當(dāng)
,當(dāng)![]() ,
,![]() 時,則
時,則![]() 的最大值為_________.
的最大值為_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地有兩個國家AAAA級景區(qū)—甲景區(qū)和乙景區(qū).相關(guān)部門統(tǒng)計了這兩個景區(qū)2019年1月至6月的客流量(單位:百人),得到如圖所示的莖葉圖.關(guān)于2019年1月至6月這兩個景區(qū)的客流量,下列結(jié)論正確的是( )
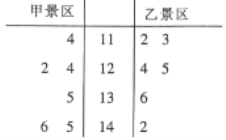
A.甲景區(qū)客流量的中位數(shù)為13000
B.乙景區(qū)客流量的中位數(shù)為13000
C.甲景區(qū)客流量的平均值比乙景區(qū)客流量的平均值小
D.甲景區(qū)客流量的極差比乙景區(qū)客流量的極差大
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某烘焙店加工一個成本為60元的蛋糕,然后以每個120元的價格出售,如果當(dāng)天賣不完,剩下的這種蛋糕作餐廚垃圾處理.
(1)若烘焙店一天加工16個這種蛋糕,求當(dāng)天的利潤![]() (單位:元)關(guān)于當(dāng)天需求量
(單位:元)關(guān)于當(dāng)天需求量![]() (單位:個,
(單位:個,![]() )的函數(shù)解析式;
)的函數(shù)解析式;
(2)為了解該種蛋糕的市場需求情況與性別是否有關(guān),隨機統(tǒng)計了100人的購買情況,得如下列聯(lián)表:
男 | 女 | 合計 | |
購買 | 15 | 35 | 50 |
不購買 | 6 | 44 | 50 |
合計 | 21 | 79 | 100 |
問:能否有![]() 的把握認(rèn)為是否購買蛋糕與性別有關(guān)?
的把握認(rèn)為是否購買蛋糕與性別有關(guān)?
附: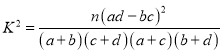
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() .
.
(1)根據(jù)![]() 不同取值,討論函數(shù)
不同取值,討論函數(shù)![]() 的奇偶性;
的奇偶性;
(2)若![]() ,對于任意的
,對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若已知![]() ,
,![]() . 設(shè)函數(shù)
. 設(shè)函數(shù)![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:![]() ,直線l過定點
,直線l過定點![]() .
.
(1)若直線l與圓C相切,求直線l的方程;
(2)若直線l與圓C相交于P,Q兩點,求![]() 的面積的最大值,并求此時直線l的方程.
的面積的最大值,并求此時直線l的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com