【題目】已知
.
（1）若
的兩根分別為某三角形兩內角的正弦值，求m的取值范圍；
（2）問是否存在實數m，使得的兩根是直角三角形兩個銳角的正弦值.
科目：高中數學 來源： 題型：
【題目】在古裝電視劇《知否》中，甲乙兩人進行一種投壺比賽，比賽投中得分情況分“有初”“貫耳”“散射”“雙耳”“依竿”五種，其中“有初”算“兩籌”，“貫耳”算“四籌”，“散射”算“五籌”，“雙耳”算“六籌”，“依竿”算“十籌”，三場比賽得籌數最多者獲勝.假設甲投中“有初”的概率為
，投中“貫耳”的概率為
，投中“散射”的概率為
，投中“雙耳”的概率為
，投中“依竿”的概率為
，乙的投擲水平與甲相同，且甲乙投擲相互獨立.比賽第一場，兩人平局;第二場，甲投了個“貫耳”，乙投了個“雙耳”，則三場比賽結束時，甲獲勝的概率為( )
A.
B.
C.D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△
的三個內角
、
、
所對應的邊分別為
、
、
，復數
，
，（其中
是虛數單位），且
.
（1）求證：
，并求邊長的值；
（2）判斷△的形狀，并求當
時，角的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且
，
.
（1）若數列是等差數列，且
，求實數
的值；
（2）若數列滿足
（
），且
，求證：是等差數列；
（3）設數列是等比數列，試探究當正實數滿足什么條件時，數列具有如下性質
：對于任意的
（），都存在
，使得
，寫出你的探究過程，并求出滿足條件的正實數的集合.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，已知PA⊥平面ABCD，且四邊形ABCD為直角梯形，∠ABC＝∠BAD＝
，PA＝AD＝2，AB＝BC＝1，點M、E分別是PA、PD的中點
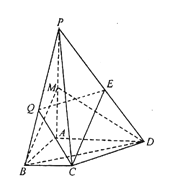
(1)求證：CE//平面BMD
(2)點Q為線段BP中點，求直線PA與平面CEQ所成角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
，在
處的切線方程為
.
（1）求
， 
；
（2）若
，證明： 
.
【答案】（1）
， 
；（2）見解析
【解析】試題分析：（1）求出函數的導數，得到關于
的方程組，解出即可；
（2）由（1）可知
， 
，
由
，可得
，令
， 利用導數研究其單調性可得
，
從而證明
.
試題解析：（（1）由題意
，所以
，
又
，所以
，
若
，則
，與
矛盾，故
， 
.
（2）由（1）可知
， 
，
由
，可得
，
令
，
，
令
當
時， 
， 
單調遞減，且
；
當
時， 
， 
單調遞增；且
，
所以
在
上當單調遞減，在
上單調遞增，且
，
故
，
故
.
【點睛】本題考查利用函數的切線求參數的方法，以及利用導數證明不等式的方法，解題時要認真審題，注意導數性質的合理運用.
【題型】解答題
【結束】
22
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
， 
為參數），以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
，若直線
與曲線
相切；
（1）求曲線
的極坐標方程；
（2）在曲線
上取兩點
， 
與原點
構成
，且滿足
，求面積
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題：
①函數
與函數
表示同一個函數；
②奇函數的圖象一定通過直角坐標系的原點；
③函數
的圖象可由
的圖象向右平移1個單位得到；
④若函數
的定義域為
，則函數
的定義域為
；
⑤設函數是在區間
上圖象連續的函數，且
，則方程
在區間上至少有一實根．
其中正確命題的序號是________．（填上所有正確命題的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的是（ ）
A.已知隨機變量
，若
.則
B.已知分類變量
與
的隨機變量
的觀察值為
，則當的值越大時，“與有關”的可信度越小.
C.在線性回歸模型中，計算其相關指數
，則可以理解為：解析變量對預報變量的貢獻率約為
D.若對于變量
與
的
組統計數據的線性回歸模型中，相關指數
.又知殘差平方和為
.那么
.（注意：
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
