
【題目】已知函數f(x)=(ax2+x﹣1)ex , 其中e是自然對數的底數,a∈R.
(Ⅰ)若a=1.求曲線f(x)在點(1,f(1))處的切線方程;
(Ⅱ)若a=﹣1,函數f(x)的圖象與函數g(x)=![]() x3+
x3+![]() x2+m的圖象有3個不同的交點,求實數m的取值范圍.
x2+m的圖象有3個不同的交點,求實數m的取值范圍.
【答案】解:(Ⅰ)∵f(x)=(x2+x﹣1)ex ,
∴f′(x)=(2x+1)ex+(x2+x﹣1)ex=(x2+3x)ex .
∴曲線f(x)在點(1,f(1))處的切線斜率k=f′(1)=4e,
∵f(1)=e,
∴曲線f(x)在點(1,f(1))處的切線方程為y﹣e=4e(x﹣1),
即4ex﹣y﹣3e=0.
(Ⅱ)令h(x)=f(x)﹣g(x)=(﹣x2+x﹣1)ex﹣(![]() x3+
x3+![]() x2+m)
x2+m)
則h′(x)=(﹣2x+1)ex+(﹣x2+x﹣1)ex﹣(x2+x)
=﹣(ex+1)(x2+x)
令h′(x)>0得﹣1<x<0,令h′(x)<0得x>0或x<﹣1.
∴h(x)在x=﹣1處取得極小值h(﹣1)=﹣![]() ﹣
﹣![]() ﹣m,在x=0處取得極大值h(0)=﹣1﹣m,
﹣m,在x=0處取得極大值h(0)=﹣1﹣m,
∵函數f(x),g(x)的圖象有三個交點,即函數h(x)有3個不同的零點,
∴![]() 即
即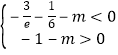 ,
,
解得:﹣![]() ﹣
﹣![]() <m<﹣1.
<m<﹣1.
【解析】(Ⅰ)求出導數,求出切線的斜率,切點,運用點斜式方程,即可得到;
(Ⅱ)令h(x)=f(x)﹣g(x),求出導數,求出單調區間,和極值,函數f(x),g(x)的圖象有三個交點,即函數h(x)有3個不同的零點,即有h(﹣1)<0,且h(0)>0,解出即可.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】某地區2007年至2013年農村居民家庭純收入![]() (單位:千元)的數據如下表:
(單位:千元)的數據如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關于![]() 的線性回歸方程;
的線性回歸方程;
(2)判斷y與![]() 之間是正相關還是負相關?
之間是正相關還是負相關?
(3)預測該地區2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為: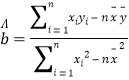 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2|cosx|sinx+sin2x,給出下列四個命題:
①函數f(x)的圖象關于直線 ![]() 對稱;
對稱;
②函數f(x)在區間 ![]() 上單調遞增;
上單調遞增;
③函數f(x)的最小正周期為π;
④函數f(x)的值域為[﹣2,2].
其中真命題的序號是 . (將你認為真命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C:![]() ,直線l:
,直線l:![]() .
.
![]() 當
當![]() 時,若圓C與直線l交于A,B兩點,過點A,B分別作l的垂線與y軸交于D,E兩點,求
時,若圓C與直線l交于A,B兩點,過點A,B分別作l的垂線與y軸交于D,E兩點,求![]() 的值;
的值;
![]() 過直線l上的任意一點P作圓的切線
過直線l上的任意一點P作圓的切線![]() 為切點
為切點![]() ,若平面上總存在定點N,使得
,若平面上總存在定點N,使得![]() ,求圓心C的橫坐標的取值范圍.
,求圓心C的橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某學校進行的一次語文與歷史成績中,隨機抽取了25位考生的成績進行分析,25位考生的語文成績已經統計在莖葉圖中,歷史成績如下:
(Ⅰ)請根據數據在莖葉圖中完成歷史成績統計;
(Ⅱ)請根據數據完成語文成績的頻數分布表及語文成績的頻率分布直方圖;
語文成績的頻數分布表:
語文成績分組 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
頻數 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣10|+|x﹣20|,且滿足f(x)<10a+10(a∈R)的解集不是空集.
(Ⅰ)求實數a的取值集合A
(Ⅱ)若b∈A,a≠b,求證aabb>abba .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上一點
上一點![]() 與橢圓右焦點的連線垂直于x軸,直線l:y=kx+m與橢圓C相交于A,B兩點(均不在坐標軸上).
與橢圓右焦點的連線垂直于x軸,直線l:y=kx+m與橢圓C相交于A,B兩點(均不在坐標軸上).
(1)求橢圓C的標準方程;
(2)設O為坐標原點,若△AOB的面積為![]() ,試判斷直線OA與OB的斜率之積是否為定值?若是請求出,若不是請說明理由.
,試判斷直線OA與OB的斜率之積是否為定值?若是請求出,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=2x2+(x﹣2a)|x﹣a|在區間[﹣3,1]上不是單調函數,則實數a的取值范圍是( )
A.[﹣4,1]
B.[﹣3,1]
C.(﹣6,2)
D.(﹣6,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的兩個焦點F1 , F2和上下兩個頂點B1 , B2是一個邊長為2且∠F1B1F2為60°的菱形的四個頂點.
(a>b>0)的兩個焦點F1 , F2和上下兩個頂點B1 , B2是一個邊長為2且∠F1B1F2為60°的菱形的四個頂點.
(1)求橢圓C的方程;
(2)過右焦點F2 , 斜率為k(k≠0)的直線與橢圓C相交于E,F兩點,A為橢圓的右頂點,直線AE,AF分別交直線x=3于點M,N,線段MN的中點為P,記直線PF2的斜率為k′.求證:kk′為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com