
【題目】如圖,某住宅小區的平面圖呈圓心角為120°的扇形AOB,小區的兩個出入口設置在點A及點C處,且小區里有一條平行于BO的小路CD,已知某人從C沿CD走到D用了10分鐘,從D沿DA走到A用了6分鐘,若此人步行的速度為每分鐘50米,求該扇形的半徑OA的長(精確到1米) 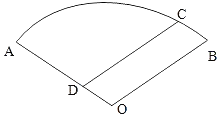
【答案】解:法一:設該扇形的半徑為r米,連接CO. 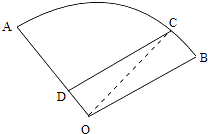
由題意,得CD=500(米),DA=300(米),∠CDO=60°
在△CDO中,CD2+OD2﹣2CDODcos60°=OC2
即, ![]()
解得 ![]() (米)
(米)
答:該扇形的半徑OA的長約為445米.
法二:連接AC,作OH⊥AC,交AC于H,
由題意,得CD=500(米),AD=300(米),∠CDA=120°
在△CDO中,AC2=CD2+AD2﹣2CDADcos120°= ![]() .
.
∴AC=700(米).![]() .
.
在直角△HAO中,AH=350(米), ![]() ,
,
∴ ![]() (米).
(米).
答:該扇形的半徑OA的長約為445米.
【解析】連接OC,由CD∥OB知∠CDO=60°,可由余弦定理得到OC的長度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某中學高三年級有學生500人,其中男生300人,女生200人。為了研究學生的數學成績是否與性別有關,采用分層抽樣的方法,從中抽取了100名學生,統計了他們期中考試的數學分數,然后按照性別分為男、女兩組,再將兩組的分數分成5組: ![]() 分別加以統計,得到如圖所示的頻率分布直方圖。
分別加以統計,得到如圖所示的頻率分布直方圖。

(I)從樣本分數小于110分的學生中隨機抽取2人,求兩人恰為一男一女的概率;
(II)若規定分數不小于130分的學生為“數學尖子生”,請你根據已知條件完成2×2列聯表,并判斷是否有90%的把握認為“數學尖子生與性別有關”?
 附表:
附表:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場計劃銷售某種產品,現邀請生產該產品的甲、乙兩個廠家進場試銷![]() 天,兩個廠家提供的返利,方案如下:甲廠家每天固定返利
天,兩個廠家提供的返利,方案如下:甲廠家每天固定返利![]() 元,且每賣出一件產品廠家再返利
元,且每賣出一件產品廠家再返利![]() 元,乙廠家無固定返利,賣出
元,乙廠家無固定返利,賣出![]() 件以內(含
件以內(含![]() 件)的產品,每件產品廠家返利
件)的產品,每件產品廠家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分別記錄其
元,分別記錄其![]() 天內的銷售件數,得到如下頻數表:
天內的銷售件數,得到如下頻數表:
甲廠家銷售件數頻數表:
銷售件數 |
|
|
|
|
|
天數 |
|
|
|
|
|
乙廠家銷售件數頻數表:
銷售件數 |
|
|
|
|
|
天數 |
|
|
|
|
|
(1) 現從甲廠家試銷的![]() 天中抽取兩天,求一天銷售量大于
天中抽取兩天,求一天銷售量大于![]() 而另一天銷售量小于
而另一天銷售量小于![]() 的概率;
的概率;
(2)若將頻率視作概率,回答以下問題:
①記乙廠家的日返利為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望;
的分布列和數學期望;
②商場擬在甲、乙兩個廠家中選擇一家長期銷售,如果僅從日返利額的角度考慮,請利用所學的統計學知識為商場作出選擇,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sinx的圖象上所有的點向右平行移動 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍(縱坐標不變),所得圖象的函數解析式是( )
個單位長度,再把所得各點的橫坐標伸長到原來的2倍(縱坐標不變),所得圖象的函數解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】暑假期間小輝計劃在8月11日至8月20日期間調研某商業中心周邊停車場停車狀況,根據停車場統計數據,該停車場在此期間“停車難易度”(即停車數量與核定的最大瞬時容量之比,40%以下為較易,40%~60%為一般,60%以上為較難),情況如圖所示,小輝隨機選擇8月11日至8月19日中的某一天達到該商業中心,并連續調研2天.
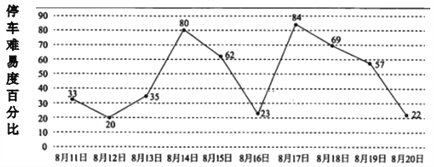
(Ⅰ)求小輝連續兩天都遇上停車場較難的概率;
(Ⅱ)設![]() 是小輝調研期間遇上停車較易的天數,求
是小輝調研期間遇上停車較易的天數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)由圖判斷從哪天開始連續三天停車難易度的方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】證明與化簡.
(1)求證:cotα=tanα+2cot2α;
(2)請利用(1)的結論證明:cotα=tanα+2tan2α+4cot4α;
(3)請你把(2)的結論推到更一般的情形,使之成為推廣后的特例,并加以證明:
(4)化簡:tan5°+2tan10°+4tan20°+8tan50°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知單調遞增的等比數列{an}滿足a2+a3+a4=28,且a3+2是a2 , a4的等差中項. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn=anlog2an , 其前n項和為Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)對于n≥2恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,若sin(A+B﹣C)=sin(A﹣B+C),則△ABC必是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+bx+c(b,c∈R),并設 ![]() ,
,
(1)若F(x)圖像在x=0處的切線方程為x﹣y=0,求b、c的值;
(2)若函數F(x)是(﹣∞,+∞)上單調遞減,則 ①當x≥0時,試判斷f(x)與(x+c)2的大小關系,并證明之;
②對滿足題設條件的任意b、c,不等式f(c)﹣Mc2≤f(b)﹣Mb2恒成立,求M的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com