
(12分)學校游園活動有這樣一個游戲項目:甲箱子里裝有3個白球、2個黑球,乙箱子里裝有1個白球、2個黑球,這些球除顏色外完全相同,每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎.(每次游戲結束后將球放回原箱)
(1)求在1次游戲中,①摸出3個白球的概率;②獲獎的概率;(6分)
(2)求在2次游戲中獲獎次數X的分布列及數學期望E(X). (6分)
(1)①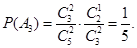 ;
②
;
②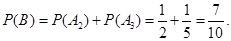 ;
;
(2)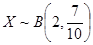 ,
,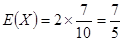
【解析】①求出基本事件總數,計算摸出3個白球事件數,利用古典概型公式,代入數據得到結果;②獲獎包含摸出2個白球和摸出3個白球,且它們互斥,根據①求出摸出2個白球的概率,再相加即可求得結果;
(2)確定在2次游戲中獲獎次數X的取值是0、1、2,求出相應的概率,即可寫出分布列,求出數學期望.
解:(1)①設“在1次游戲中摸出i個白球”為事件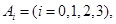
則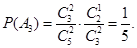 …………………2分
…………………2分
②設“在1次游戲中獲獎”為事件B,則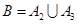 ,A2,A3互斥,
,A2,A3互斥,
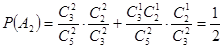 …………………4分
…………………4分
所以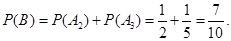 …………………6分
…………………6分
(2)法Ⅰ解:由題意可知X的所有可能取值為0,1,2. ……………7分
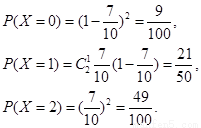
……………………………………………10分
所以X的分布列是
|
X |
0 |
1 |
2 |
|
P |
|
|
|
X的數學期望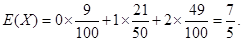 ……………12分
……………12分
法Ⅱ: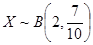 ,于是可依次得
,于是可依次得
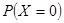 ,
,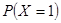 ,
,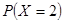 ;
;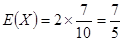


 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省揚州市寶應縣高三下學期期初測試數學試卷 題型:解答題
(本題滿分10分)學校游園活動有這樣一個游戲項目:甲箱子里裝有3個白球、2個黑球;乙箱子里裝有1個白球、2個黑球,這些球除顏色外完全相同,每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎.(每次游戲結束后將球放回原箱)
(1)求在1次游戲中,
①摸出3個白球的概率;
②獲獎的概率;
(2)求在兩次游戲中獲獎次數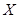 的分布列及數學期望
的分布列及數學期望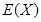 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分13分)
學校游園活動有這樣一個游戲項目:甲箱子里裝有3個白球、2個黑球,乙箱子里裝有1個白球、2個黑球,這些球除顏色外完全相同,每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎.(每次游戲結束后將球放回原箱)
(Ⅰ)求在1次游戲中,
(i)摸出3個白球的概率;
(ii)獲獎的概率;
(Ⅱ)求在2次游戲中獲獎次數![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com