
已知函數
(1)當 時,求函數
時,求函數 的最小值和最大值
的最小值和最大值
(2)設三角形角 的對邊分別為
的對邊分別為 且
且 ,
,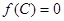 ,若
,若 ,求
,求 的值.
的值.
(1)最小值為 ,最大值為0;(2)
,最大值為0;(2) .
.
解析試題分析:(1)先通過三角函數的恒等變形化 的形式后再解答;一般地,涉及三角函數的值域問題,多數情況下要將其變形為
的形式后再解答;一般地,涉及三角函數的值域問題,多數情況下要將其變形為 后,再利用三角函數的性質解答,也有部分題目,可轉化為角的某個三角函數,然后用換元法轉化為非三角函數問題;(2)由
后,再利用三角函數的性質解答,也有部分題目,可轉化為角的某個三角函數,然后用換元法轉化為非三角函數問題;(2)由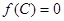 先求出
先求出 ,再利用正弦定理求出
,再利用正弦定理求出 ,再利用余弦定理則可求出
,再利用余弦定理則可求出 .在三角形中求角或邊,通常對條件進行“統一”,統一為邊或統一為角,主要的工具是正弦定理和余弦定理,同時不要忘記了三角形內角和定理.
.在三角形中求角或邊,通常對條件進行“統一”,統一為邊或統一為角,主要的工具是正弦定理和余弦定理,同時不要忘記了三角形內角和定理.
試題解析:(1)
 ,因為
,因為  ,
, ,所以當
,所以當 時,
時, 取得最小值
取得最小值 ,當
,當 時,
時, 取得最大值0 6分
取得最大值0 6分
(2)由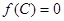 ,得
,得 ,又
,又 為三角形內角,所以
為三角形內角,所以 ,所以
,所以 ,由正弦定理結合
,由正弦定理結合 得,
得, ,再由余弦定理
,再由余弦定理 得,
得,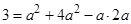 ,解得
,解得 ,所以
,所以 13分
13分
考點:三角函數性質、正弦定理、余弦定理.


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)如圖,在△ABC中,∠ABC=90°,AB= ,BC=1,P為△ABC內一點,∠BPC=90°
,BC=1,P為△ABC內一點,∠BPC=90°
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,有兩座建筑物AB和CD都在河的對岸(不知 道它們的高度,且不能到達對岸),某人想測量兩 座建筑物尖頂A、C之間的距離,但只有卷尺和測 角儀兩種工具.若此人在地面上選一條基線EF,用 卷尺測得EF的長度為a,并用測角儀測量了一些角度: ,
, ,
, ,
, ,
, 請你用文字和公式寫出計算A、C之間距離的步驟和結果.
請你用文字和公式寫出計算A、C之間距離的步驟和結果.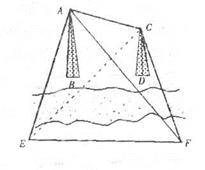
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com