Question

【題目】某廠生產不同規格的一種產品，根據檢測標準，其合格產品的質量與尺寸之間近似滿足關系式為大于0的常數).按照某項指標測定，當產品質量與尺寸的比在區間內時為優等品.現隨機抽取6件合格產品，測得數據如下:

尺寸	38	48	58	68	78	88
質量	16.8	18.8	20.7	22.4	24	25.5
質量與尺寸的比	0.442	0.392	0.367	0.329	0.308	0.290

(I)現從抽取的6件合格產品中再任選3件，記為取到優等品的件數，試求隨機變量的分布列和期望;

(II)根據測得數據作了初步處理，得相關統計量的值如下表:

75.3	24.6	18.3	101.4

(i)根據所給統計量，求關于的回歸方程;

(ii)已知優等品的收益(單位:千元)與的關系為，則當優等品的尺寸為何值時，收益的預報值最大? (精確到0.1)

附:對于樣本， 其回歸直線的斜率和截距的最小二乘估計公式分別為：

Answer 1

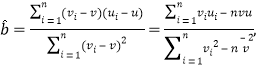
【答案】（1）見解析（2）(i)，(ii)

【解析】分析：（1）要求隨機變量的分布列，應先確定抽取的6件合格產品中，優等品的件數，應確定區間的大致范圍，即。進而由抽取6件合格產品的測得數據可得有3件為優等品，3件為非優等品。所以取到優等品的件數，進而求這四種取值時的概率，進而可得分布列。用期望公式即可求得期望。（2）(i)因為中的與之間不是直線性回歸關系，故兩邊取對數可得，換元令，得且，根據題中所給的表中數據可求出

進而可求得求得

所求關于的回歸方程為。(ii)要求當優等品的尺寸為何值時，收益的預報值最大。應用來表示收益。故將代入可得。

可令，則可變為，這個是關于的二次函數，要求其最大值，應先求自變量的取值范圍。由優等品質量與尺寸的比可求得，進而可得，即。將配方可得 。由二次函數的性質可知當時，取最大值。進而可求當優等品的尺寸，收益的預報值最大。

詳解：（1）解：由已知，優等品的質量與尺寸的比在區間內，即

則隨機抽取的6件合格產品中，有3件為優等品，3件為非優等品

現從抽取的6件合格產品中再任選3件，則取到優等品的件數

的分布列為

	0	1	2	3

（2）解：(i)對兩邊取自然對數得，

令得且

根據所給統計量及最小乘估計公式有，

得得

所求關于的回歸方程為可知，

（ii)由（i)，，則

由優等品質量與尺寸的比即

令

當時，取最大值

即優等品的尺寸，收益的預報值最大.