
【題目】在直角坐標系xOy中,已知點P(![]() ,1),直線l的參數方程為
,1),直線l的參數方程為 (t為參數)若以O為極點,以Ox為極軸,選擇相同的單位長度建立極坐標系,則曲線C的極坐標方程為ρ=
(t為參數)若以O為極點,以Ox為極軸,選擇相同的單位長度建立極坐標系,則曲線C的極坐標方程為ρ=![]() cos(θ-
cos(θ-![]() )
)
(Ⅰ)求直線l的普通方程和曲線C的直角坐標方程;
(Ⅱ)設直線l與曲線C相交于A,B兩點,求點P到A,B兩點的距離之積.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(I)由加減消元法可將直線l的參數方程化為普通方程;由![]() 可將曲線C的極坐標方程化為直角坐標方程.
可將曲線C的極坐標方程化為直角坐標方程.
(II)把直線l的參數方程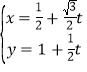 ,代入圓的方程可得
,代入圓的方程可得![]() ,由于點P(
,由于點P(![]() ,1)在直線l上,可得|PA||PB|=|t1t2|.利用韋達定理可得結果
,1)在直線l上,可得|PA||PB|=|t1t2|.利用韋達定理可得結果
試題解析:解:(I)由直線l的參數方程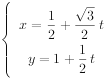 ,消去參數t,可得
,消去參數t,可得![]() =0;
=0;
由曲線C的極坐標方程ρ=![]() cos(θ-
cos(θ-![]() )展開為
)展開為![]() ,
,
化為ρ2=ρcosθ+ρsinθ,
∴曲線C的直角坐標方程為x2+y2=x+y,即![]() =
=![]() .
.
(II)把直線l的參數方程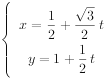 代入圓的方程可得
代入圓的方程可得![]() =0,
=0,
∵點P(![]() ,1)在直線l上,∴|PA||PB|=|t1t2|=
,1)在直線l上,∴|PA||PB|=|t1t2|=![]() .
.


科目:高中數學 來源: 題型:
【題目】為了監控某種零件的一條生產線的生產過程,檢驗員每隔30 min從該生產線上隨機抽取一個零件,并測量其尺寸(單位:cm).下面是檢驗員在一天內依次抽取的16個零件的尺寸:
抽取順序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi為抽取的第i個零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相關系數r,并回答是否可以認為這一天生產的零件尺寸不隨生產
過程的進行而系統地變大或變小(若|r|<0.25,則可以認為零件的尺寸不隨生產過程的進行而系統地
變大或變小).
(2)一天內抽檢零件中,如果出現了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就認為這條生產線在這一天
+3s)之外的零件,就認為這條生產線在這一天
的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
①從這一天抽檢的結果看,是否需對當天的生產過程進行檢查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的數據稱為離群值,試剔除離群值,估計這條生產線當天生產的零件尺寸的
+3s)之外的數據稱為離群值,試剔除離群值,估計這條生產線當天生產的零件尺寸的
均值與標準差.(精確到0.01)
附:樣本(xi,yi)(i=1,2,…,n)的相關系數r=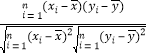 ,
,![]() ≈0.09.
≈0.09.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1=1,nan+1﹣(n+1)an=1(n∈N+)
(1)求數列{an}的通項公式;
(2)若 ![]() ,求數列{bn}的最大項.
,求數列{bn}的最大項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() ,x∈R.
,x∈R.
(1)證明對a、b∈R,且a≠b,總有:|f(a)﹣f(b)|<|a﹣b|;
(2)設a、b、c∈R,且 ![]() ,證明:a+b+c≥ab+bc+ca.
,證明:a+b+c≥ab+bc+ca.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足f(x+2)=2f(x),且當x∈[2,4]時, 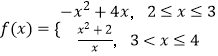 ,g(x)=ax+1,對x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),則實數a的取值范圍為( )
,g(x)=ax+1,對x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),則實數a的取值范圍為( )
A.![]()
B.![]()
C.(0,8]
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年存節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過600 元(含600元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種. 方案一:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,一次性摸出3個球,其中獎規則為:若摸到3個紅球,享受免單優惠;若摸到2個紅球,則打6折;若摸到1個紅球,則打7折;若沒摸到紅球,則不打折.
方案二:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,有放回每次摸取1球,連摸3次,每摸到1次紅球,立減200元.
(1)若兩個顧客均分別消費了 600元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿1000元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】調查某醫院某段時間內嬰兒出生的時間與性別的關系,得到下面的數據:出生時間在晚上的男嬰為24人,女嬰為8人;出生時間在白天的男嬰為31人,女嬰為26人.
(1)將2×2列聯表補充完整.
性別 | 出生時間 | 總計 | |
晚上 | 白天 | ||
男嬰 | |||
女嬰 | |||
總計 | |||
(2)能否在犯錯誤的概率不超過0.1的前提下認為嬰兒性別與出生時間有關系?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足:
(1)函數y=f(x﹣1)的圖象關于點(1,0)對稱;
(2)對x∈R,f( ![]() ﹣x)=f(
﹣x)=f( ![]() +x)成立
+x)成立
(3)當x∈(﹣ ![]() ,﹣
,﹣ ![]() ]時,f(x)=log2(﹣3x+1),則f(2011)=( )
]時,f(x)=log2(﹣3x+1),則f(2011)=( )
A.﹣5
B.﹣4
C.﹣3
D.﹣2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com