
(09年湖北鄂州5月模擬理)已知兩定點A(-3,0),B(3,0),動圓M與直線AB相切于點N,且![]() ,現分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
,現分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
⑴求動點P的軌跡方程;
⑵若直線xmy3=0截動點P的軌跡所得的弦長為5,求m的值;
⑶設過軌跡上的點P的直線與兩直線解析:⑴由題設及平面幾何知識得![]()
∴動點P的軌跡是以A、B為焦點的雙曲線右支由![]() ,
,
∴b2=c2-a2=5,故所求P點的軌跡方程為![]() 3分
3分
⑵易知直線xmy3=0恒過雙曲線焦點B(3,0)
設該直線與雙曲線右支相交于D(xD,yD),E(xE,yE)由雙曲線第二定義知
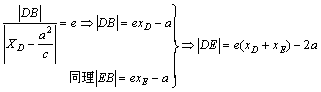 ,又a=2,c=3,
,又a=2,c=3,
∴e=![]() 則
則![]() 5分
5分
由|DE|=5,得![]() ,從而易知僅當m=0時,
,從而易知僅當m=0時,![]() 滿足|DE|=5
滿足|DE|=5
故所求m=0 7分
⑶設P(x,y),P1(x1、y1),P2(x2、y2)且P分有向線段![]() 所成的比為λ,則
所成的比為λ,則
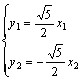 ,
,![]() 又點P(x,y)在雙曲線
又點P(x,y)在雙曲線
![]() 上,∴
上,∴![]() ,化簡得
,化簡得![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() 9分
9分
令![]() ∵
∵![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,
上單增,
又![]() ∴
∴![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,∴umin=u(1)=4,
上單增,∴umin=u(1)=4,
又![]() ,
,![]() ∴umin=
∴umin=![]()


科目:高中數學 來源: 題型:
(09年湖北鄂州5月模擬理)(12分)如圖,已知四棱錐P―ABCD,底面ABCD為菱形,PA⊥平面ABCD,∠ABC=60o,E、F 分別是BC、PC的中點.
⑴證明:AE⊥PD;
⑵若H為PD上的動點,EH與平面PAD所成最大角的正
切值為![]() ,求二面角E―AF―C的余弦值.
,求二面角E―AF―C的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
(09年湖北鄂州5月模擬理)(14分)設函數![]() .
.![]()
⑴求f (x)的單調區間和極值;
⑵是否存在實數a,使得關于x的不等式f (x)≥a的解集為(0,+∞)?若存在,求a的取值范圍;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年湖北鄂州5月模擬文)(13分)設f (x)=![]() ,方程f (x)=x有唯一解,數列{xn}滿足f (x1)=1,
,方程f (x)=x有唯一解,數列{xn}滿足f (x1)=1,
xn+1=f (xn)(n∈N*).
⑴求數列{xn}的通項公式;
⑵已知數列{an}滿足查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com