Question

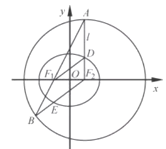
【題目】如圖，在平面直角坐標系xOy中，橢圓C:的焦點為F1（–1、0），

F2（1，0）．過F2作x軸的垂線l，在x軸的上方，l與圓F2:交于點A，與橢圓C交于點D.連結AF1并延長交圓F2于點B，連結BF2交橢圓C于點E，連結DF1．已知DF1=．

（1）求橢圓C的標準方程；

（2）求點E的坐標．

Answer 1

【答案】（1）；

（2）.

【解析】

(1)由題意分別求得a,b的值即可確定橢圓方程；

(2)解法一：由題意首先確定直線的方程，聯立直線方程與圓的方程，確定點B的坐標，聯立直線BF2與橢圓的方程即可確定點E的坐標；

解法二：由題意利用幾何關系確定點E的縱坐標，然后代入橢圓方程可得點E的坐標.

（1）設橢圓C的焦距為2c.

因為F1(－1，0)，F2(1，0)，所以F1F2=2，c=1.

又因為DF1=，AF2⊥x軸，所以DF2=，

因此2a=DF1+DF2=4，從而a=2.

由b2=a2-c2，得b2=3.

因此，橢圓C的標準方程為.

（2）解法一：

由（1）知，橢圓C：，a=2，

因為AF2⊥x軸，所以點A的橫坐標為1.

將x=1代入圓F2的方程(x-1) 2+y2=16，解得y=±4.

因為點A在x軸上方，所以A(1，4).

又F1(-1，0)，所以直線AF1：y=2x+2.

由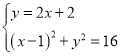，得，

解得或.

將代入，得，

因此.又F2(1，0)，所以直線BF2：.

由，得，解得或.

又因為E是線段BF2與橢圓的交點，所以.

將代入，得.因此.

解法二：

由（1）知，橢圓C：.如圖，連結EF1.

因為BF2=2a，EF1+EF2=2a，所以EF1=EB，

從而∠BF1E=∠B.

因為F2A=F2B，所以∠A=∠B，

所以∠A=∠BF1E，從而EF1∥F2A.

因為AF2⊥x軸，所以EF1⊥x軸.

因為F1(-1，0)，由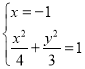，得.

又因為E是線段BF2與橢圓的交點，所以.

因此.