
【題目】如圖,矩形![]() 和梯形
和梯形![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() ,
,![]() .
.
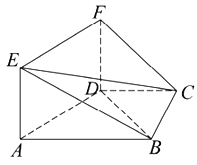
(1)求證:![]() 平面
平面![]() ;
;
(2)當![]() 的長為何值時,直線
的長為何值時,直線![]() 與平面
與平面![]() 所成角的大小為45°?
所成角的大小為45°?
【答案】(1)答案見解析(2)![]()
【解析】
(1)(法一)以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 建系.根據三角形相似可得
建系.根據三角形相似可得![]() ,故由勾股定理可知
,故由勾股定理可知![]() .求得面
.求得面![]() 的法向量
的法向量![]() ,再由向量的數量積求得
,再由向量的數量積求得![]() ,可得證;
,可得證;
(法二)由矩形和梯形的幾何性質得出線線平行,再由面面平行的判定定理可證得面![]() 面
面![]() ,由面面平行的性質可得證;
,由面面平行的性質可得證;
(2)由(1)可得面BCE的法向量![]() ,由線面角的向量計算方法建立方程可求得.
,由線面角的向量計算方法建立方程可求得.
(1)(法一)如圖,以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 建系.
建系.
設![]() ,由
,由![]() ,
,![]() ,
,![]() ,依據三角形相似可得
,依據三角形相似可得![]() ,故由勾股定理可知
,故由勾股定理可知![]() .
.
在![]() 中,可得
中,可得![]() .
.
所以各點坐標為![]() .
.
![]() ,設面
,設面![]() 的法向量為
的法向量為![]() ,所以
,所以 ,
,
化簡得![]() ,令
,令![]() 得
得![]() ,得
,得![]() ,故
,故![]() .
.
又![]() 不在面
不在面![]() 上,所以
上,所以![]() 面
面![]() .
.
(法二)
因為矩形![]() ,故
,故![]() .又
.又![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() 在面
在面![]() 上,
上,![]()
![]() 在面
在面![]() 上,故面
上,故面![]() 面
面![]() .
.
又![]() 在面
在面![]() 上,且
上,且![]() 不在面
不在面![]() 上,故
上,故![]() 面
面![]() .
.
(2)![]() ,
,
設面![]() 法向量為
法向量為![]() ,所以
,所以 ,化簡得
,化簡得 ,令
,令![]() ,得
,得![]() .
.
由題得 .
.
故![]() ,因為
,因為![]() 為正,所以
為正,所以![]() .
.



科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,
,![]() ,
,![]() ,
,![]() 是橢圓上任意三點,
是橢圓上任意三點,![]() ,
,![]() 關于原點對稱且滿足
關于原點對稱且滿足![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)若斜率為![]() 的直線與圓:
的直線與圓:![]() 相切,與橢圓
相切,與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() 、
、![]() ,求
,求![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由我國引領的5G時代已經到來,5G的發展將直接帶動包括運營、制造、服務在內的通信行業整體的快速發展,進而對GDP增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合圖,下列說法不正確的是( )
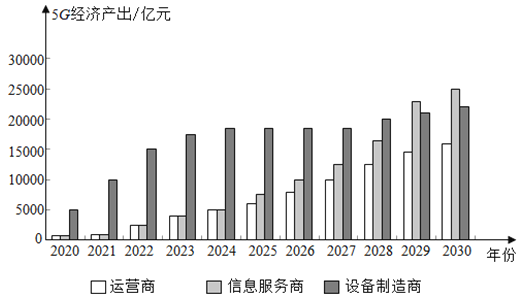
A.5G的發展帶動今后幾年的總經濟產出逐年增加
B.設備制造商的經濟產出前期增長較快,后期放緩
C.設備制造商在各年的總經濟產出中一直處于領先地位
D.信息服務商與運營商的經濟產出的差距有逐步拉大的趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
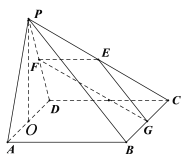
(Ⅰ)求證:PO平面![]() ;
;
(Ⅱ)求平面EFG與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,若存在,求線段
,若存在,求線段![]() 的長度;若不存在,說明理由.
的長度;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在傳染病學中,通常把從致病刺激物侵入機體或者對機體發生作用起,到機體出現反應或開始呈現該疾病對應的相關癥狀時止的這一階段稱為潛伏期. 一研究團隊統計了某地區1000名患者的相關信息,得到如下表格:
潛伏期(單位:天) |
|
|
|
|
|
|
|
人數 |
|
|
|
|
|
|
|
(1)求這1000名患者的潛伏期的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)該傳染病的潛伏期受諸多因素的影響,為研究潛伏期與患者年齡的關系,以潛伏期是否超過6天為標準進行分層抽樣,從上述1000名患者中抽取200人,得到如下列聯表. 請將列聯表補充完整,并根據列聯表判斷是否有![]() 的把握認為潛伏期與患者年齡有關;
的把握認為潛伏期與患者年齡有關;
潛伏期 | 潛伏期 | 總計 | |
50歲以上(含50歲) |
| ||
50歲以下 | 55 | ||
總計 | 200 |
(3)以這1000名患者的潛伏期超過6天的頻率,代替該地區1名患者潛伏期超過6天發生的概率,每名患者的潛伏期是否超過6天相互獨立. 為了深入研究,該研究團隊隨機調查了![]() 名患者,其中潛伏期超過6天的人數最有可能(即概率最大)是多少?
名患者,其中潛伏期超過6天的人數最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年11月份,全國工業生產者出廠價格同比下降![]() ,環比下降
,環比下降![]() 某企業在了解市場動態之后,決定根據市場動態及時作出相應調整,并結合企業自身的情況作出相應的出廠價格,該企業統計了2019年1~10月份產品的生產數量
某企業在了解市場動態之后,決定根據市場動態及時作出相應調整,并結合企業自身的情況作出相應的出廠價格,該企業統計了2019年1~10月份產品的生產數量![]() (單位:萬件)以及銷售總額
(單位:萬件)以及銷售總額![]() (單位:十萬元)之間的關系如下表:
(單位:十萬元)之間的關系如下表:
| 2.08 | 2.12 | 2.19 | 2.28 | 2.36 | 2.48 | 2.59 | 2.68 | 2.80 | 2.87 |
| 4.25 | 4.37 | 4.40 | 4.55 | 4.64 | 4.75 | 4.92 | 5.03 | 5.14 | 5.26 |
(1)計算![]() 的值;
的值;
(2)計算相關系數![]() ,并通過
,并通過![]() 的大小說明
的大小說明![]() 與
與![]() 之間的相關程度;
之間的相關程度;
(3)求![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,并推測當產量為3.2萬件時銷售額為多少.(該問中運算結果保留兩位小數)
,并推測當產量為3.2萬件時銷售額為多少.(該問中運算結果保留兩位小數)
附:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為
中的斜率和截距的最小二乘估計公式分別為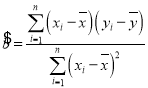 ,
,![]() ;
;
相關系數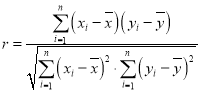 .
.
參考數據: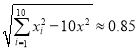 ,
,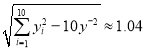 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且過點
,且過點![]() .
.
(1)求橢圓的方程;
(2)已知![]() ,是否存在k使得點A關于l的對稱點B(不同于點A)在橢圓C上?若存在求出此時直線l的方程,若不存在說明理由.
,是否存在k使得點A關于l的對稱點B(不同于點A)在橢圓C上?若存在求出此時直線l的方程,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 平行于直線
平行于直線![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩個不同的點,若
兩個不同的點,若![]() 為鈍角,求直線
為鈍角,求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com