
【題目】已知數列![]() 的前
的前![]() 項和
項和![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(1)證明:![]() 是等比數列,并求
是等比數列,并求![]() ;
;
(2)若數列![]() 中去掉與數列
中去掉與數列![]() 中相同的項后,余下的項按原順序排列成數列
中相同的項后,余下的項按原順序排列成數列![]() ,求
,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】國家正積極推行垃圾分類工作,教育部辦公廳等六部門也發布了《關于在學校推進生活垃圾分類管理工作的通知》.《通知》指出,到2020年底,各學校生活垃圾分類知識普及率要達到100%某市教育主管部門據此做了“哪些活動最能促進學生進行垃圾分類”的問卷調查(每個受訪者只能在問卷的4個活動中選擇一個)如圖是調查結果的統計圖,以下結論正確的是( )
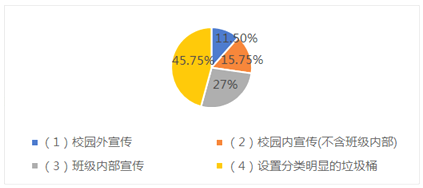
A.回答該問卷的受訪者中,選擇的(2)和(3)人數總和比選擇(4)的人數多
B.回該問卷的受訪者中,選擇“校園外宣傳”的人數不是最少的
C.回答該問卷的受訪者中,選擇(4)的人數比選擇(2)的人數可能多30人
D.回答該問卷的總人數不可能是1000人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() ).下面表格所確定的點
).下面表格所確定的點![]() 中,恰有三個點在橢圓
中,恰有三個點在橢圓![]() 上.
上.
|
|
| 1 |
|
|
| 0 |
|
|
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為坐標原點,點
為坐標原點,點![]() ,
,![]() 分別為
分別為![]() 的上下頂點,直線
的上下頂點,直線![]() 經過
經過![]() 的右頂點
的右頂點![]() ,且與
,且與![]() 的另一個公共點為
的另一個公共點為![]() ,直線
,直線![]() ,
,![]() 相交于點
相交于點![]() ,若
,若![]() 與
與![]() 軸的交點
軸的交點![]() 異于
異于![]() ,
,![]() ,證明
,證明![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差不為0的等差數列,
是公差不為0的等差數列,![]() ,數列
,數列![]() 是等比數列,且
是等比數列,且![]() ,
,![]() ,
,![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設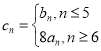 ,求
,求![]() 的前n項和
的前n項和![]() ;
;
(3)若![]() 對
對![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019新型冠狀病毒感染的肺炎的傳播有飛沫、氣溶膠、接觸等途徑,為了有效抗擊疫情,隔離性防護是一項具體有效措施.某市為有效防護疫情,宣傳居民盡可能不外出,鼓勵居民的生活必需品可在網上下單,商品由快遞業務公司統一配送(配送費由政府補貼).快遞業務主要由甲公司與乙公司兩家快遞公司承接:“快遞員”的工資是“底薪+送件提成”.這兩家公司對“快遞員”的日工資方案為:甲公司規定快遞員每天底薪為70元,每送件一次提成1元;乙公司規定快遞員每天底薪為120元,每日前83件沒有提成,超過83件部分每件提成5元,假設同一公司的快遞員每天送件數相同,現從這兩家公司往年忙季各隨機抽取一名快遞員并調取其100天的送件數,得到如下條形圖:

(1)求乙公司的快遞員一日工資y(單位:元)與送件數n的函數關系;
(2)若將頻率視為概率,回答下列問題:
①記甲公司的“快遞員”日工資為X(單位:元).求X的分布列和數學期望;
②小王想到這兩家公司中的一家應聘“快遞員”的工作,如果僅從日收入的角度考慮,請你利用所學過的統計學知識為他作出選擇,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com