
【題目】【2018廣東深圳市高三一模】已知橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 與橢圓有且只有一個交點
與橢圓有且只有一個交點![]() .
.
(I)求橢圓![]() 的方程和點
的方程和點![]() 的坐標;
的坐標;
(II) ![]() 為坐標原點,與
為坐標原點,與![]() 平行的直線
平行的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
, ![]() ,求
,求![]() 的面積最大時直線
的面積最大時直線![]() 的方程.
的方程.
【答案】(I)橢圓![]() 的方程為
的方程為![]() ,點
,點![]() 的坐標為
的坐標為![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】試題分析:(1) 根據橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 與橢圓有且只有一個交點,結合性質
與橢圓有且只有一個交點,結合性質![]() ,列出關于
,列出關于![]() 、
、![]() 、
、![]() 的方程組,求出
的方程組,求出![]() 、
、![]() 、
、![]() ,即可得結果;(2) 設直線
,即可得結果;(2) 設直線![]() 的方程為
的方程為![]() ,設
,設![]() ,
, ![]() ,聯立
,聯立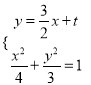 消去
消去![]() ,利用韋達定理,弦長公式以及點到直線距離公式與三角形面積公式可得
,利用韋達定理,弦長公式以及點到直線距離公式與三角形面積公式可得![]() ,利用二次函數的性質可得結果.
,利用二次函數的性質可得結果.
試題解析:(1)由![]() ,得
,得![]() ,故
,故![]() .
.
則橢圓![]() 的方程為
的方程為![]() .
.
由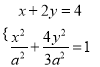 ,消去
,消去![]() ,得
,得![]() .①
.①
由![]() ,得
,得![]() .
.
故橢圓![]() 的方程為
的方程為![]() .
.
所以![]() ,所以點
,所以點![]() 的坐標為
的坐標為![]() ;
;
(2)設直線![]() 的方程為
的方程為![]() ,
,
設![]() ,
, ![]() ,聯立
,聯立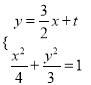 消去
消去![]() ,得
,得![]() ,
,
則有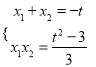 ,
,
由![]() ,得
,得![]() ,
,
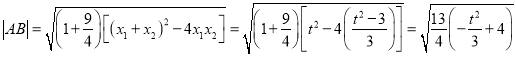 .
.
設原點到直線![]() 的距離為
的距離為![]() .
.
則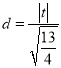 .
.
所以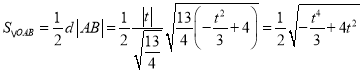 .
.
所以當![]() 時,即
時,即![]() 時,
時, ![]() 的面積最大.
的面積最大.
所以直線![]() 的方程為
的方程為![]() 或
或![]() .
.
【方法點晴】本題主要考查待定系數求橢圓方程以及直線與橢圓的位置關系和數量積公式,屬于難題.用待定系數法求橢圓方程的一般步驟;①作判斷:根據條件判斷橢圓的焦點在![]() 軸上,還是在
軸上,還是在![]() 軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程
軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程![]() 或
或![]()
![]() ;③找關系:根據已知條件,建立關于
;③找關系:根據已知條件,建立關于![]() 、
、![]() 、
、![]() 的方程組;④得方程:解方程組,將解代入所設方程,即為所求.
的方程組;④得方程:解方程組,將解代入所設方程,即為所求.


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:
【題目】下列所給4個圖象中,與所給3件事吻合最好的順序為 ( )
①我離開學校不久,發現自己把作業本忘在教室,于是立刻返回教室里取了作業本再回家;
②我放學回家騎著車一路以常速行駛,只是在途中遇到一次交通堵塞,耽擱了一些時間;

③我放學從學校出發后,心情輕松,緩緩行進,后來為了趕時間開始加速.
A.(1)(2)(4)B.(4)(1)(2)C.(4)(1)(3)D.(4)(2)(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李明自主創業,在網上經營一家水果店,銷售的水果中有草莓、京白梨、西瓜、桃,價格依次為60元/盒、65元/盒、80元/盒、90元/盒.為增加銷量,李明對這四種水果進行促銷:一次購買水果的總價達到120元,顧客就少付x元.每筆訂單顧客網上支付成功后,李明會得到支付款的80%.
①當x=10時,顧客一次購買草莓和西瓜各1盒,需要支付__________元;
②在促銷活動中,為保證李明每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() (x
(x![]() R),g(x)=2a-1
R),g(x)=2a-1
(1)求函數f(x)的單調區間與極值.
(2)若f(x)≥g(x)對![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是正三角形的三棱錐![]() 中,D 為PC的中點,
中,D 為PC的中點,![]() ,
,![]()

(1)求證:![]() 平面
平面![]() ;
;
(2)求 BD 與平面 ABC 所成角的大小;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校選派甲、乙、丙、丁、戊5名學生代表學校參加市級“演講”和“詩詞”比賽,下面是他們的一段對話.甲說:“乙參加‘演講’比賽”;乙說:“丙參加‘詩詞’比賽”;丙說“丁參加‘演講’比賽”;丁說:“戊參加‘詩詞’比賽”;戊說:“丁參加‘詩詞’比賽”.
已知這5個人中有2人參加“演講”比賽,有3人參加“詩詞”比賽,其中有2人說的不正確,且參加“演講”的2人中只有1人說的不正確.根據以上信息,可以確定參加“演講”比賽的學生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 平面
平面![]() ,點
,點![]() 在以
在以![]() 為直徑的
為直徑的![]() 上,
上,![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)設二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】試題分析:
(1)由△ABC中位線的性質可得![]() ,則
,則![]() 平面
平面![]() .由線面平行的判斷定理可得
.由線面平行的判斷定理可得![]() 平面
平面![]() .結合面面平行的判斷定理可得
.結合面面平行的判斷定理可得![]() 平面
平面![]() .
.
(2)由圓的性質可得![]() ,由線面垂直的性質可得
,由線面垂直的性質可得![]() ,據此可知
,據此可知![]() 平面
平面![]() .利用面面垂直的判斷定理可得平面
.利用面面垂直的判斷定理可得平面![]() 平面
平面![]() .
.
(3)以![]() 為坐標原點,
為坐標原點,![]() 所在的直線為
所在的直線為![]() 軸,
軸,![]() 所在的直線為
所在的直線為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() .結合空間幾何關系計算可得平面
.結合空間幾何關系計算可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的一個法向量
的一個法向量![]() ,則
,則![]() .由圖可知
.由圖可知![]() 為銳角,故
為銳角,故![]() .
.
試題解析:
(1)證明:因為點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 的中點,
的中點,
所以![]() ,因為
,因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)證明:因為點![]() 在以
在以![]() 為直徑的
為直徑的![]() 上,所以
上,所以![]() ,即
,即![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)解:如圖,以![]() 為坐標原點,
為坐標原點,![]() 所在的直線為
所在的直線為![]() 軸,
軸,![]() 所在的直線為
所在的直線為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() .
.
因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
延長![]() 交
交![]() 于點
于點![]() .因為
.因為![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
設平面![]() 的法向量
的法向量![]() .
.
因為 ,所以
,所以![]() ,即
,即![]() .
.
令![]() ,則
,則![]() ,
,![]() .
.
所以![]() .
.
同理可求平面![]() 的一個法向量
的一個法向量![]() .
.
所以![]() .由圖可知
.由圖可知![]() 為銳角,所以
為銳角,所以![]() .
.

【題型】解答題
【結束】
21
【題目】已知圓![]() ,點
,點![]() ,直線
,直線![]() .
.
(1)求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;
垂直的直線方程;
(2)在直線![]() 上(
上(![]() 為坐標原點),存在定點
為坐標原點),存在定點![]() (不同于點
(不同于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com