
【題目】如圖所示的幾何體中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 為
為![]() 的中點,
的中點,![]() ,四邊形
,四邊形![]() 為矩形,線段
為矩形,線段![]() 交
交![]() 于點
于點![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)見解析(2)![]() (3)在線段
(3)在線段![]() 上存在一點
上存在一點![]() 滿足題意,且
滿足題意,且![]()
【解析】
(1)由題意結合線面平行的判定定理即可證得題中的結論;
(2)建立空間直角坐標系,利用兩個半平面的法向量可得二面角的余弦值,然后利用同角三角函數(shù)基本關系可得二面角的正弦值;
(3)假設點Q存在,利用直線的方向向量和平面的法向量計算可得點Q的存在性和位置.
(1)因為四邊形![]() 為矩形,所以
為矩形,所以![]() 為
為![]() 的中點.連接
的中點.連接![]() ,
,
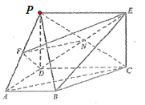
在![]() 中,
中,![]() 分別為
分別為![]() 的中點,所以
的中點,所以![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)易知![]() 兩兩垂直,如圖以
兩兩垂直,如圖以![]() 為原點,分別以
為原點,分別以![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
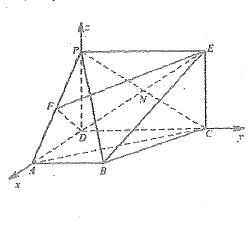
則![]() ,所以
,所以![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則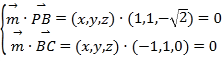 即
即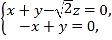 解得
解得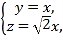
令![]() ,得
,得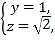
所以平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
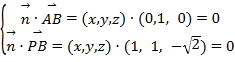 ,據(jù)此可得
,據(jù)此可得 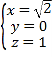 ,
,
則平面![]() 的一個法向量為
的一個法向量為![]() ,
,
![]() ,于是
,于是![]() .
.
故二面角![]() 的正弦值為
的正弦值為![]() .
.
(3)設存在點![]() 滿足條件.
滿足條件.
由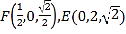 ,
,
設![]() ,整理得
,整理得 ,
,
則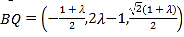 .
.
因為直線![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ,
,
所以
解得![]() ,
,
由![]() 知
知![]() ,即點
,即點![]() 與
與![]() 重合.
重合.
故在線段![]() 上存在一點
上存在一點![]() ,且
,且![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】共享單車給市民出行帶來了諸多便利,某公司購買了一批單車投放到某地給市民使用.據(jù)市場分析,每輛單車的營運累計收入![]() (單位:元)與營運天數(shù)
(單位:元)與營運天數(shù)![]() 滿足
滿足![]() .
.
(1)要使營運累計收入高于800元,求營運天數(shù)的取值范圍;
(2)每輛單車營運多少天時,才能使每天的平均營運收入最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線![]() ,
, ![]() .
.
(1)當![]() 時,直線
時,直線![]() 過
過![]() 與
與![]() 的交點,且它在兩坐標軸上的截距相反,求直線
的交點,且它在兩坐標軸上的截距相反,求直線![]() 的方程;
的方程;
(2)若坐標原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,判斷
,判斷![]() 與
與![]() 的位置關系.
的位置關系.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為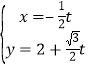 (
(![]() 為參數(shù)),以原點為極點,以
為參數(shù)),以原點為極點,以![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,
(Ⅰ)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() ,曲線
,曲線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]()
![]() 的左,右焦點
的左,右焦點![]() ,
,![]() ,上頂點為
,上頂點為![]() ,
,![]() ,
,![]() 為橢圓上任意一點,且
為橢圓上任意一點,且![]() 的面積最大值為
的面積最大值為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若點![]() .
.![]() 為橢圓
為橢圓![]() 上的兩個不同的動點,且
上的兩個不同的動點,且![]() (
(![]() 為坐標原點),則是否存在常數(shù)
為坐標原點),則是否存在常數(shù)![]() ,使得
,使得![]() 點到直線
點到直線![]() 的距離為定值?若存在,求出常數(shù)
的距離為定值?若存在,求出常數(shù)![]() 和這個定值;若不存在,請說明理由.
和這個定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 是雙曲線
是雙曲線![]() 上一點,
上一點, ![]() 分別是雙曲線
分別是雙曲線![]() 的左、右頂點,直線
的左、右頂點,直線![]() 的斜率之積為
的斜率之積為![]() .
.
(1)求雙曲線的離心率;
(2)過雙曲線![]() 的右焦點且斜率為
的右焦點且斜率為![]() 的直線交雙曲線于
的直線交雙曲線于![]() 兩點,
兩點, ![]() 為坐標原點,
為坐標原點, ![]() 為雙曲線上一點,滿足
為雙曲線上一點,滿足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 為橢圓的左、右焦點,點
為橢圓的左、右焦點,點![]() 在直線
在直線![]() 上且不在
上且不在![]() 軸上,直線
軸上,直線![]() 與橢圓的交點分別為
與橢圓的交點分別為![]() 和
和![]() ,
,![]() 為坐標原點.
為坐標原點.
![]() 設直線
設直線![]() 的斜率為
的斜率為![]() ,證明:
,證明:![]()
![]() 問直線
問直線![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 的斜率
的斜率![]() 滿足
滿足![]() ?若存在,求出所有滿足條件的點
?若存在,求出所有滿足條件的點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在心理學研究中,常采用對比試驗的方法評價不同心理暗示對人的影響,具體方法如下:將參加試驗的志愿者隨機分成兩組,一組接受甲種心理暗示,另一組接受乙種心理暗示,通過對比這兩組志愿者接受心理暗示后的結果來評價兩種心理暗示的作用,現(xiàn)有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,從中隨機抽取5人接受甲種心理暗示,另5人接受乙種心理暗示.
(I)求接受甲種心理暗示的志愿者中包含A1但不包含![]() 的頻率。
的頻率。
(II)用X表示接受乙種心理暗示的女志愿者人數(shù),求X的分布列與數(shù)學期望EX.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com