
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c,且bsinA= ![]() acosB. (Ⅰ)求角B的大小;
acosB. (Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面積.
【答案】解:(Ⅰ)在△ABC中,∵bsinA= ![]() acosB, ∴由正弦定理可得 sinBsinA=
acosB, ∴由正弦定理可得 sinBsinA= ![]() sinAcosB.
sinAcosB.
∵sinA≠0,∴sinB= ![]() cosB,∴tanB=
cosB,∴tanB= ![]() ,∴B=
,∴B= ![]() .
.
(Ⅱ)∵sinC=2sinA,∴c=2a,
由余弦定理b2=a2+c2﹣2accosB,即9=a2+4a2﹣2a2acos ![]() ,
,
解得a= ![]() ,c=2a=2
,c=2a=2 ![]() .
.
故△ABC的面積為 ![]() acsinB=
acsinB= ![]()
【解析】(Ⅰ)在△ABC中,由 bsinA= ![]() acosB,利用正弦定理求得tanB的值,可得B的值.(Ⅱ)由條件利用正弦定理得c=2a,再由余弦定理b2=a2+c2﹣2accosB,求得a的值,可得c=2a的值,根據 △ABC的面積為
acosB,利用正弦定理求得tanB的值,可得B的值.(Ⅱ)由條件利用正弦定理得c=2a,再由余弦定理b2=a2+c2﹣2accosB,求得a的值,可得c=2a的值,根據 △ABC的面積為 ![]() acsinB,計算求得結果.
acsinB,計算求得結果.
【考點精析】認真審題,首先需要了解正弦定理的定義(正弦定理:![]() ).
).


科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對邊分別為a,b,c,已知 ![]() . (Ⅰ)若b=
. (Ⅰ)若b= ![]() ,當△ABC周長取最大值時,求△ABC的面積;
,當△ABC周長取最大值時,求△ABC的面積;
(Ⅱ)設 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考北京文數】已知橢圓C:![]() 過點A(2,0),B(0,1)兩點.
過點A(2,0),B(0,1)兩點.
(I)求橢圓C的方程及離心率;
(Ⅱ)設P為第三象限內一點且在橢圓C上,直線PA與y軸交于點M,直線PB與x軸交于點N,求證:四邊形ABNM的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017屆湖南省長沙市高三上學期統一模擬考試文數】已知過![]() 的動圓恒與
的動圓恒與![]() 軸相切,設切點為
軸相切,設切點為![]() 是該圓的直徑.
是該圓的直徑.
(Ⅰ)求![]() 點軌跡
點軌跡![]() 的方程;
的方程;
(Ⅱ)當![]() 不在y軸上時,設直線
不在y軸上時,設直線![]() 與曲線
與曲線![]() 交于另一點
交于另一點![]() ,該曲線在
,該曲線在![]() 處的切線與直線
處的切線與直線![]() 交于
交于![]() 點.求證:
點.求證: ![]() 恒為直角三角形.
恒為直角三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對一批底部周長屬于[80,130](單位:cm)的樹木進行研究,從中隨機抽出200株樹木并測出其底部周長,得到頻率分布直方圖如圖所示,由此估計,這批樹木的底部周長的眾數是cm,中位數是cm,平均數是cm. 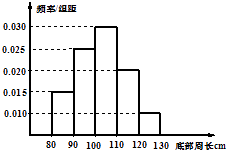
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
: ![]() 相切,且與圓
相切,且與圓![]() :
: ![]() 相內切,記圓心
相內切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .設
.設![]() 為曲線
為曲線![]() 上的一個不在
上的一個不在![]() 軸上的動點,
軸上的動點, ![]() 為坐標原點,過點
為坐標原點,過點![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() ,
, ![]() 兩個不同的點.
兩個不同的點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)試探究![]() 和
和![]() 的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
(Ⅲ)記![]() 的面積為
的面積為![]() ,
, ![]() 的面積為
的面積為![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com