
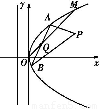
如圖所示,在直角坐標(biāo)系xOy中,點P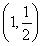 到拋物線C:y2=2px(p>0)的準(zhǔn)線的距離為
到拋物線C:y2=2px(p>0)的準(zhǔn)線的距離為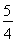 .點M(t,1)是C上的定點,A,B是C上的兩動點,且線段AB被直線OM平分.
.點M(t,1)是C上的定點,A,B是C上的兩動點,且線段AB被直線OM平分.
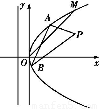
(1)求p,t的值;
(2)求△ABP面積的最大值.
(1)  (2)
(2) 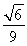
【解析】
解:(1)由題意知 得
得
(2)由(1)知M(1,1),
直線OM的方程為y=x,
設(shè)A(x1,y1),B(x2,y2),線段AB的中點為Q(m,m).
由題意知,
設(shè)直線AB的斜率為k(k≠0).
由
得(y1-y2)(y1+y2)=x1-x2,
故k·2m=1,
所以直線AB的方程為y-m=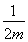 (x-m),
(x-m),
即x-2my+2m2-m=0.
由 消去x,
消去x,
整理得y2-2my+2m2-m=0,
所以Δ=4m-4m2>0,
y1+y2=2m,y1y2=2m2-m.
從而|AB|=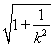 ·|y1-y2|=
·|y1-y2|= ·
· .
.
設(shè)點P到直線AB的距離為d,
則d= .
.
設(shè)△ABP的面積為S,則
S=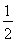 |AB|·d=|1-2(m-m2)|·
|AB|·d=|1-2(m-m2)|·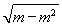 .
.
由Δ=4m-4m2>0,得0<m<1.
令u=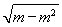 ,0<u≤
,0<u≤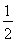 ,則S=u(1-2u2).
,則S=u(1-2u2).
設(shè)S(u)=u(1-2u2),0<u≤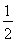 ,則S′(u)=1-6u2.
,則S′(u)=1-6u2.
由S′(u)=0,得u=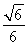 ∈
∈ ,
,
因此S(u)在 單調(diào)遞增,在
單調(diào)遞增,在 單調(diào)遞減,
單調(diào)遞減,
所以S(u)max=S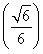 =
=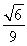 .
.
故△ABP面積的最大值為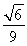 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
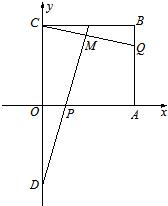 如圖所示,在直角坐標(biāo)平面上的矩形OABC中,|OA|=2,| OC |=
如圖所示,在直角坐標(biāo)平面上的矩形OABC中,|OA|=2,| OC |=| 3 |
| OP |
| λOA |
| AQ |
| AB |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2012•大豐市一模)如圖所示,在直角坐標(biāo)平面內(nèi),反比例函數(shù)的圖象經(jīng)過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.
(2012•大豐市一模)如圖所示,在直角坐標(biāo)平面內(nèi),反比例函數(shù)的圖象經(jīng)過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年湖南省高考適應(yīng)性測試數(shù)學(xué)試卷(文科)(解析版) 題型:解答題
 ,點P,Q滿足
,點P,Q滿足 ,
, ,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年高考數(shù)學(xué)模擬試卷(文科)(解析版) 題型:解答題
 ,點P,Q滿足
,點P,Q滿足 ,
, ,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年江蘇省連云港市東海高級中學(xué)高考數(shù)學(xué)考前猜題試卷(1)(解析版) 題型:解答題
 ,點P,Q滿足
,點P,Q滿足 ,
, ,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
,點D是C關(guān)于原點的對稱點,直線DP與CQ相交于點M.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com