
【題目】如圖,四棱錐P﹣ABCD中,PA⊥平面ABCD,四邊形ABCD為梯形,AD∥BC,BC=6,PA=AD=CD=2,E為BC上一點且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 
(1)求證:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
【答案】
(1)證明:∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE,
又∵PB⊥AE,PB∩PA=P,
∴AE⊥平面PAB,又∵AB平面PAB,
∴AE⊥AB.
又∵PA⊥AB,PA∩AE=A,
∴AB⊥平面PAE,
又∵PE平面PAE,
∴AB⊥PE.
(2)解:以A為坐標原點,建立如圖所示的空間直角坐標系A﹣xyz,
則B(2 ![]() ,0,0),P(0,0,2),C(﹣
,0,0),P(0,0,2),C(﹣ ![]() ,3,0),D(﹣
,3,0),D(﹣ ![]() ,1,0),
,1,0),
∴ ![]() =(﹣3
=(﹣3 ![]() ,3,0),
,3,0), ![]() =(﹣
=(﹣ ![]() ,3,﹣2),
,3,﹣2), ![]() =(0,2,0).
=(0,2,0).
設平面PBC的一個法向量 ![]() =(x,y,z),
=(x,y,z),
則 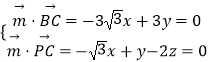 ,令x=1,得
,令x=1,得 ![]() =(1,
=(1, ![]() ,
, ![]() ).
).
同理可求平面PCD的一個法向量 ![]() =(2,0,﹣
=(2,0,﹣ ![]() ).
).
∴cos ![]() >=
>= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∵二面角B﹣PC﹣D為鈍二面角,
∴二面角B﹣PC﹣D的余弦值為﹣ ![]() .
.

【解析】(1)推導出PA⊥AE,AE⊥AB.由此能證明AB⊥PE.(2)以A為坐標原點,建立空間直角坐標系A﹣xyz,利用向量法能求出二面角B﹣PC﹣D的余弦值.
【考點精析】根據題目的已知條件,利用棱錐的結構特征的相關知識可以得到問題的答案,需要掌握側面、對角面都是三角形;平行于底面的截面與底面相似,其相似比等于頂點到截面距離與高的比的平方.


科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() :
:![]() ,點
,點![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() (不在y軸上).
(不在y軸上).

(1)若直線![]() 的斜率為3,求
的斜率為3,求![]() 的長度;
的長度;
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,求證:
,求證:![]() 為定值,并求出該定值;
為定值,并求出該定值;
(3)設![]() 的中點為
的中點為![]() ,是否存在直線
,是否存在直線![]() ,使得
,使得![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】旅行社為去廣西桂林的某旅游團包飛機去旅游,其中旅行社的包機費為10000元,旅游團中的每人的飛機票按以下方式與旅行社結算:若旅游團的人數在20或20以下,飛機票每人收費800元;若旅游團的人數多于20,則實行優惠方案,每多1人,機票費每張減少10元,但旅游團的人數最多為75,則該旅行社可獲得利潤的最大值為( )
A. 12000元B. 15000元C. 12500元D. 20000元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 分別是
分別是![]() 的中點將
的中點將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 重合于點
重合于點![]() .則下列結論正確的是( )
.則下列結論正確的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值為
的余弦值為![]()
D. 點![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某3D打印機,其打出的產品質量按照百分制衡量,若得分不低于85分則為合格品,低于85分則為不合格品,商家用該打印機隨機打印了15件產品,得分情況如圖; 
(1)寫出該組數據的中位數和眾數,并估計該打印機打出的產品為合格品的概率;
(2)若打印一件合格品可獲利54元,打印一件不合格品則虧損18元,記X為打印3件產品商家所獲得的利潤,在(1)的前提下,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某3D打印機,其打出的產品質量按照百分制衡量,若得分不低于85分則為合格品,低于85分則為不合格品,商家用該打印機隨機打印了15件產品,得分情況如圖; 
(1)寫出該組數據的中位數和眾數,并估計該打印機打出的產品為合格品的概率;
(2)若打印一件合格品可獲利54元,打印一件不合格品則虧損18元,記X為打印3件產品商家所獲得的利潤,在(1)的前提下,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經國務院批復同意,鄭州成功入圍國家中心城市,某校學生團針對“鄭州的發展環境”對20名學生進行問卷調查打分(滿分100分),得到如圖1所示莖葉圖.
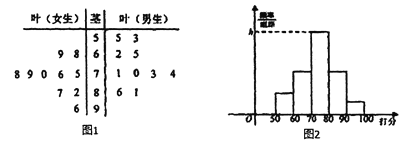
(1)分別計算男生女生打分的平均分,并用數學特征評價男女生打分的數據分布情況;
(2)如圖2按照打分區間![]() 繪制的直方圖中,求最高矩形的高;
繪制的直方圖中,求最高矩形的高;
(3)從打分在70分以下(不含70分)的同學中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的左焦點
的左焦點![]() 左頂點
左頂點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知![]() ,
,![]() 是橢圓上的兩點,
是橢圓上的兩點,![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點.若
兩側的動點.若![]() ,試問直線
,試問直線![]() 的斜率是否為定值?請說明理由.
的斜率是否為定值?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com