
已知函數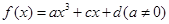 是R上的奇函數,當
是R上的奇函數,當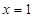 時
時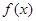 取得極值
取得極值 .
.
(I)求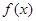 的單調區間和極大值
的單調區間和極大值
(II)證明對任意
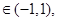 不等式
不等式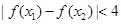 恒成立.
恒成立.
(Ⅰ)單增區間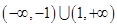 ,單減區間
,單減區間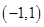 ,極大值
,極大值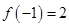 ;(Ⅱ)見解析.
;(Ⅱ)見解析.
解析試題分析:(Ⅰ)根據奇函數的定義可知 ,由此解得
,由此解得 ,由已知條件“當
,由已知條件“當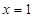 時
時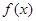 取得極值
取得極值 ”可得
”可得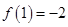 以及
以及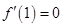 ,聯立方程組解得
,聯立方程組解得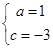 ,寫出函數的解析式為
,寫出函數的解析式為 ,然后對函數
,然后對函數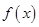 求導,利用函數的單調性與導數的關系判斷函數
求導,利用函數的單調性與導數的關系判斷函數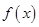 在實數集R上的單調性,并由此得到函數
在實數集R上的單調性,并由此得到函數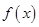 在
在 處取得極大值;(Ⅱ)根據函數
處取得極大值;(Ⅱ)根據函數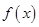 在區間
在區間 是單調遞減的,可知函數
是單調遞減的,可知函數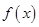 在區間
在區間 上的極大值
上的極大值 和極小值
和極小值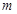 ,從而由對任意的
,從而由對任意的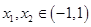 都有不等式
都有不等式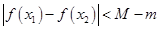 成立,即得結論.
成立,即得結論.
試題解析:(Ⅰ)由奇函數的定義,有 ,
,
即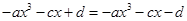 ,∴
,∴ .
.
因此 ,
,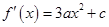 ,
,
由條件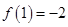 為
為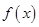 的極值,必有
的極值,必有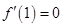 .
.
故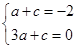 ,解得
,解得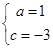 . 4分
. 4分
因此,  ,
,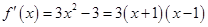 ,
, .
.
當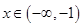 時,
時,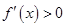 ,故
,故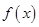 在單調區間
在單調區間 上是增函數;
上是增函數;
當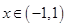 時,
時,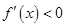 ,故
,故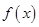 在單調區間
在單調區間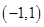 上是減函數;
上是減函數;
當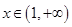 時,
時,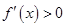 ,故
,故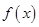 在單調區間
在單調區間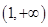 上是增函數.
上是增函數.
∴函數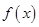 在
在 處取得極大值,極大值為
處取得極大值,極大值為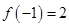 . 8分
. 8分
(Ⅱ)由(I)知, 是減函數,
是減函數,
且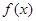 在
在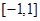 上的最大值
上的最大值
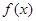 在
在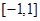 上的最小值
上的最小值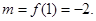
∴對任意 恒有
恒有 12分
12分
考點:1.求函數的解析式;2.利用導數研究函數的單調性;3.利用導數研究函數的極值;4.解不等式;5.奇函數的性質


科目:高中數學 來源: 題型:解答題
如圖,某自來水公司要在公路兩側排水管,公路為東西方向,在路北側沿直線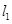 排水管,在路南側沿直線
排水管,在路南側沿直線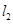 排水管(假設水管與公路的南,北側在一條直線上且水管的大小看作為一條直線),現要在矩形區域ABCD內沿直線EF將
排水管(假設水管與公路的南,北側在一條直線上且水管的大小看作為一條直線),現要在矩形區域ABCD內沿直線EF將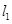 與
與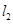 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60 m,公路兩側排管費用為每米1萬元,穿過公路的EF部分的排管費用為每米2萬元,設EF與AB所成角為
m,公路兩側排管費用為每米1萬元,穿過公路的EF部分的排管費用為每米2萬元,設EF與AB所成角為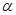 .矩形區域內的排管費用為W.
.矩形區域內的排管費用為W.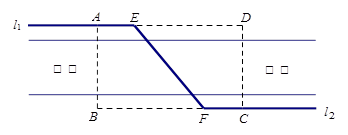
(1)求W關于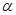 的函數關系式;
的函數關系式;
(2)求W的最小值及相應的角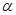 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
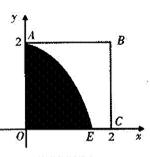
如圖,某小區有一邊長為2(單位:百米)的正方形地塊OABC,其中OAE是一個游泳池,計劃在地塊OABC內修一條與池邊AE相切的直路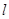 (寬度不計),切點為M,并把該地塊分為兩部分.現以點O為坐標原點,以線段OC所在直線為x軸,建立平面直角坐標系,若池邊AE滿足函數
(寬度不計),切點為M,并把該地塊分為兩部分.現以點O為坐標原點,以線段OC所在直線為x軸,建立平面直角坐標系,若池邊AE滿足函數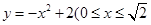 的圖象,且點M到邊OA距離為
的圖象,且點M到邊OA距離為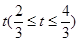 .
.
(1)當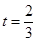 時,求直路
時,求直路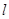 所在的直線方程;
所在的直線方程;
(2)當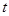 為何值時,地塊OABC在直路
為何值時,地塊OABC在直路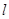 不含泳池那側的面積取到最大,最大值是多少?
不含泳池那側的面積取到最大,最大值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某自來水公司要在公路兩側鋪設水管,公路為東西方向,在路北側沿直線鋪設線路l1,在路南側沿直線鋪設線路l2,現要在矩形區域ABCD內沿直線將l1與l2接通.已知AB = 60m,BC = 80m,公路兩側鋪設水管的費用為每米1萬元,穿過公路的EF部分鋪設水管的費用為每米2萬元,設∠EFB= α,矩形區域內的鋪設水管的總費用為W.
(1)求W關于α的函數關系式;
(2)求W的最小值及相應的角α.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com