
【題目】在四棱錐P﹣ABCD中,AD∥BC,AD=AB=DC=![]()
![]() BC=1,E是PC的中點,面PAC⊥面ABCD.
BC=1,E是PC的中點,面PAC⊥面ABCD.
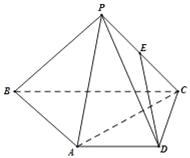
(1)證明:ED∥面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(Ⅰ)證明過程如解析;(Ⅱ)![]()
【解析】試題分析:(Ⅰ)取PB的中點F,連接AF,EF,由三角形的中位線定理可得四邊形ADEF是平行四邊形.得到DE∥AF,再由線面平行的判定可得ED∥面PAB;(Ⅱ)法一、取BC的中點M,連接AM,由題意證得A在以BC為直徑的圓上,可得AB⊥AC,找出二面角A-PC-D的平面角.求解三角形可得二面角A-PC-D的余弦值.
試題解析:(Ⅰ)證明:取PB的中點F,連接AF,EF.
∵EF是△PBC的中位線,∴EF∥BC,且EF=![]()
![]() .
.
又AD=BC,且AD=![]()
![]() ,∴AD∥EF且AD=EF,
,∴AD∥EF且AD=EF,
則四邊形ADEF是平行四邊形.
∴DE∥AF,又DE面ABP,AF面ABP,∴ED∥面PAB
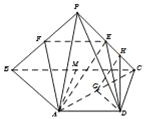
(Ⅱ)法一、取BC的中點M,連接AM,則AD∥MC且AD=MC,
∴四邊形ADCM是平行四邊形,
∴AM=MC=MB,則A在以BC為直徑的圓上.∴AB⊥AC,可得![]()
![]() .
.
過D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,則DG⊥PC.
過G作GH⊥PC于H,則PC⊥面GHD,連接DH,則PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中,![]() ,連接AE,
,連接AE,![]() .
.
在Rt△GDH中,![]() ,
,
∴![]() ,
,
即二面角A﹣PC﹣D的余弦值![]()
法二、取BC的中點M,連接AM,則AD∥MC,且AD=MC.
∴四邊形ADCM是平行四邊形,
∴AM=MC=MB,則A在以BC為直徑的圓上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
如圖以A為原點,![]() 方向分別為x軸正方向,y軸正方向建立空間直角坐標系.
方向分別為x軸正方向,y軸正方向建立空間直角坐標系.
可得![]() ,
,![]() .
.
設P(x,0,z),(z>0),依題意有![]() ,
,![]() ,
,
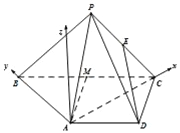
解得![]() .
.
則![]() ,
,![]() ,
,![]() .
.
設面PDC的一個法向量為![]() ,
,
由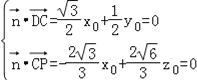 ,取x0=1,得
,取x0=1,得![]() .
.
![]()
![]() 為面PAC的一個法向量,且
為面PAC的一個法向量,且![]() ,
,
設二面角A﹣PC﹣D的大小為θ,
則有![]() ,即二面角A﹣PC﹣D的余弦值
,即二面角A﹣PC﹣D的余弦值![]() .
.


科目:高中數學 來源: 題型:
【題目】已知復數z1= ![]() +(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虛數單位).
+(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虛數單位).
(1)若復數z1﹣z2在復平面上對應點落在第一象限,求實數a的取值范圍;
(2)若虛數z1是實系數一元二次方程x2﹣6x+m=0的根,求實數m值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:f(x)=2 ![]() cos2x+sin2x﹣
cos2x+sin2x﹣ ![]() +1(x∈R).求:
+1(x∈R).求:
(1)f(x)的最小正周期;
(2)f(x)的單調增區間;
(3)若x∈[﹣ ![]() ,
, ![]() ]時,求f(x)的值域.
]時,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2﹣2x﹣8≤0},B={x| ![]() <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌茶壺的原售價為80元/個,今有甲、乙兩家茶具店銷售這種茶壺,甲店用如下方法促銷:如果只購買一個茶壺,其價格為78元/個;如果一次購買兩個茶壺,其價格為76元/個;…,一次購買的茶壺數每增加一個,那么茶壺的價格減少2元/個,但茶壺的售價不得低于44元/個;乙店一律按原價的75%銷售.現某茶社要購買這種茶壺x個,如果全部在甲店購買,則所需金額為y1元;如果全部在乙店購買,則所需金額為y2元.
(1)分別求出y1、y2與x之間的函數關系式;
(2)該茶社去哪家茶具店購買茶壺花費較少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|(x﹣a),a為實數.
(1)若函數f(x)為奇函數,求實數a的值;
(2)若函數f(x)在[0,2]為增函數,求實數a的取值范圍;
(3)是否存在實數a(a<0),使得f(x)在閉區間 ![]() 上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
上的最大值為2,若存在,求出a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x||x﹣a|≤3,x∈R},B={x|x2﹣3x﹣4>0,x∈R}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某倉庫為了保持庫內的濕度和溫度,四周墻上均裝有如圖所示的自動通風設施.該設施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等邊三角形,固定點E為AB的中點.△EMN是由電腦控制其形狀變化的三角通風窗(陰影部分均不通風),MN是可以沿設施邊框上下滑動且始終保持和AB平行的伸縮橫桿. 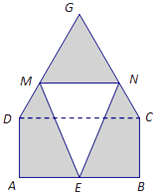
(1)設MN與AB之間的距離為x米,試將△EMN的面積S(平方米)表示成關于x的函數;
(2)求△EMN的面積S(平方米)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com