【題目】設函數
.
(1)若當
時，
取得極值，求
的值，并求的單調區間.
(2)若存在兩個極值點
，求的取值范圍，并證明：
.
科目：高中數學 來源： 題型：
【題目】已知直線
過橢圓
的右焦點，且交橢圓于A，B兩點，線段AB的中點是
，
（1）求橢圓的方程；
（2）過原點的直線l與線段AB相交（不含端點）且交橢圓于C，D兩點，求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐E﹣ABCD的側棱DE與四棱錐F﹣ABCD的側棱BF都與底面ABCD垂直，AD⊥CD，AB∥CD，AB＝3，AD＝4，AE＝5，
．
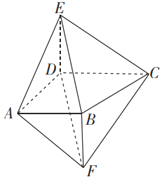
（1）證明：DF∥平面BCE．
（2）求A到平面BEDF的距離，并求四棱錐A﹣BEDF的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
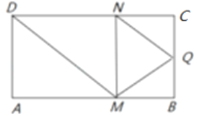
【題目】如圖，矩形
中，
，
，
為
的中點，點
，
分別在線段
，
上運動（其中不與
，
重合，不與
，
重合），且
，沿
將
折起，得到三棱錐
，則三棱錐體積的最大值為______；當三棱錐體積最大時，其外接球的半徑
______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校藝術節對
四件參賽作品只評一件一等獎，在評獎揭曉前，甲，乙，丙，丁四位同學對這四件參賽作品預測如下：
甲說：“是
或
作品獲得一等獎”； 乙說：“ 
作品獲得一等獎”；
丙說：“ 
兩件作品未獲得一等獎”； 丁說：“是作品獲得一等獎”．
評獎揭曉后，發現這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是_________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據（單位：m3）和使用了節水龍頭50天的日用水量數據，得到頻數分布表如下：
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
（1）在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖：
（2）估計該家庭使用節水龍頭后，日用水量小于0.35 m3的概率；
（3）估計該家庭使用節水龍頭后，一年能節省多少水？（一年按365天計算，同一組中的數據以這組數據所在區間中點的值作代表．）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝|x﹣2|+|x+1|．
（1）解關于x的不等式f（x）≤5；
（2）若函數f（x）的最小值記為m，設a，b，c均為正實數，且a+4b+9c＝m，求
的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
