【題目】已知△ABC的角A、B、C所對的邊分別是a、b、c，設向量 
， 
， 
．
（1）若 
∥ 
，求證：△ABC為等腰三角形；
（2）若 ⊥ 
，邊長c=2，角C= 
，求△ABC的面積．
【答案】
（1）證明：∵m∥n
∴asinA=bsinB
即a 
=b 
．其中R為△ABC外接圓半徑．
∴a=b
∴△ABC為等腰三角形
（2）解：由題意，mp=0
∴a（b﹣2）+b（a﹣2）=0
∴a+b=ab
由余弦定理4=a2+b2﹣2abcos 
∴4=a2+b2﹣ab=（a+b）2﹣3ab
∴（ab）2﹣3ab﹣4=0
∴ab=4或ab=﹣1（舍去）
∴S△ABC= 
absinC
= ×4×sin = 
【解析】（1）利用向量平行的條件，寫出向量平行坐標形式的條件，得到關于三角形的邊和角之間的關系，利用余弦定理變形得到三角形是等腰三角形．（2）利用向量垂直數量積為零，寫出三角形邊之間的關系，結合余弦定理得到求三角形面積所需的兩邊的乘積的值，求出三角形的面積．
智趣暑假溫故知新系列答案科目：高中數學 來源： 題型：
【題目】如圖，正三棱柱
所有棱長都是2，D棱AC的中點，E是
棱的中點，AE交
于點H.
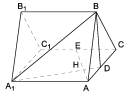
（1）求證：
平面
；
（2）求二面角
的余弦值；
（3）求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列4個命題，其中正確的命題序號為（ ）
①|x+ 
|的最小值是2 ② 
的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2．
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在等腰梯形
中， 
， 
， 
，四邊形
為矩形， 
，平面
平面
，點
為線段
中點．
（Ⅰ）求異面直線
與
所成的角的正切值；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量（
噸）與相應的生產能耗
（噸）標準煤的幾組對照數據：
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 6 | 9 | 10 |
（1）請畫出上表數據的散點圖；
（2）請根據上表提供的數據，用最小二乘法求出關于的線性回歸方程
；
（3）已知該廠技術改造前100噸甲產品能耗為200噸標準煤，試根據（2）求出的線性回歸方程，預測生產100噸甲產品的生產能耗比技術改造前降低多少噸標準煤？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
.
（1）若橢圓
的右焦點坐標為
，求
的值；
（2）由橢圓
上不同三點構成三角形稱為橢圓的內接三角形.若以
為直角頂點的橢圓
的內接等腰直角三角形恰有三個，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是一個正方體的展開圖，如果將它還原為正方體，那么NC、DE、AF、BM這四條線段所在的直線是異面直線的有多少對？試以其中一對為例進行證明．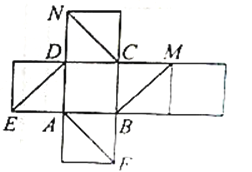
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
