
設![]() 是定義在
是定義在![]() 上以2為周期的函數,對
上以2為周期的函數,對![]() ,用
,用![]() 表示區間
表示區間![]() .
.
已知當![]() 時,函數
時,函數![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)對自然數![]() ,求集合
,求集合![]() {
{![]() 使方程
使方程![]() 在
在![]() 上有兩個不相等的實根}
上有兩個不相等的實根}
(1)![]()
(2)[1] 當![]() 時,
時, ![]()
![]() 或
或![]()
![]() ;
;
[2] 當![]() 時,
時, ![]()
![]()
![]() ;
;
[3] 當![]() 時,
時, ![]()
![]()
![]()
(1)因為![]() 是以2為周期的函數,所以當
是以2為周期的函數,所以當![]() 時,
時,![]() 是
是![]() 的周期函數
的周期函數
又當![]() 時,
時,![]() ,所以
,所以![]() ,
,
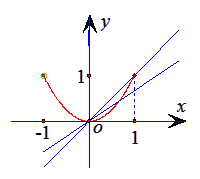 即當
即當![]() ,
,![]() 時,
時,![]() . ………………3分;
. ………………3分;
(2)[1] 當![]() 時,
時, ![]() 表示區間
表示區間![]() , 此時
, 此時![]() , 令
, 令![]() 則欲使方程
則欲使方程![]() 有兩個不等根,即使
有兩個不等根,即使![]() 與
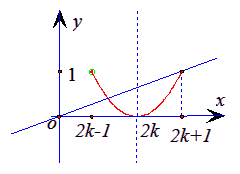
與![]() 這兩個函數圖像有兩個不同交點.如圖所示,
這兩個函數圖像有兩個不同交點.如圖所示,
只要:![]()
![]() 或
或![]()
![]() 即可………5分
即可………5分
 [2] 當
[2] 當![]() 時,
時, ![]() 表示區間
表示區間![]() , 此時
, 此時![]() , 令
, 令![]() 則欲使方程
則欲使方程![]() 有兩個不等根,即使
有兩個不等根,即使![]() 與
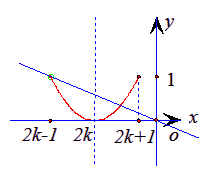
與![]() 這兩個函數圖像有兩個不同交點.如圖所示,
這兩個函數圖像有兩個不同交點.如圖所示,
只要:![]()
![]()
![]() 即可……….7分
即可……….7分
 [3] 當
[3] 當![]() 時,
時, ![]() 表示區間
表示區間![]() , 此時
, 此時![]() , 令
, 令![]() 則欲使方程
則欲使方程![]() 有兩個不等根,即使
有兩個不等根,即使![]() 與
與![]() 這兩個函數圖像有兩個不同交點.如圖所示,
這兩個函數圖像有兩個不同交點.如圖所示,
只要:![]()
![]()
![]() 即可……………9分
即可……………9分
綜上所述:[1] 當![]() 時,
時, ![]()
![]() 或
或![]()
![]() ;
;
[2] 當![]() 時,
時, ![]()
![]()
![]() ;
;
[3] 當![]() 時,
時, ![]()
![]()
![]() ……………10分
……………10分
注: 本題還可以用“根的分布”的方法,請酌情給分.


科目:高中數學 來源:2012-2013學年寧夏高三第六次考試理科數學試卷(解析版) 題型:選擇題
設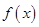 是定義在
是定義在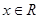 上以2為周期的偶函數,已知
上以2為周期的偶函數,已知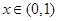 ,
,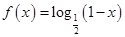 ,則函數
,則函數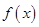 在
在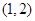 上( )
上( )
A.是增函數且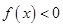 B.是增函數且
B.是增函數且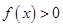
C.是減函數且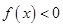 D.是減函數且
D.是減函數且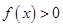
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省高三第三次月考文科數學試卷 題型:選擇題
設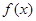 是定義在
是定義在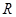 上以2為周期的偶函數,當
上以2為周期的偶函數,當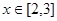 時,
時,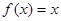 則
則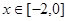 時
時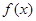 的解析式為 (
)
的解析式為 (
)
A.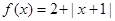 B.
B.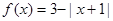
|
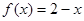 D.
D.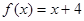
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com