Question

【題目】已知函數(shù)（），的部分圖象如圖所示，且，則（ ）

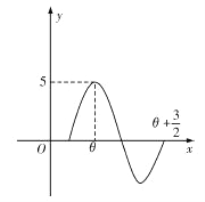
A. 6 B. 4 C. -4 D. -6

Answer 1

【答案】D

【解析】分析：利用三角函數(shù)恒等變換的應(yīng)用化簡函數(shù)解析式可得f（x）=5sin（2ωx﹣φ）﹣1，其中sinφ=，cosφ=，由函數(shù)圖象可求周期T，由f（x0）=4，利用正弦函數(shù)的對稱性可求sin[2ω（x0+1）﹣φ）=﹣1，利用正弦函數(shù)的周期性進而可求f（x0+1）的值．

詳解：∵f（x）=6sinωxcosωx﹣8cos2ωx+3

=3sin2ωx﹣4cos2ωx﹣1

=5sin（2ωx﹣φ）﹣1，其中sinφ=，cosφ=，

∴設(shè)函數(shù)f（x）的最小正周期為T，則T=（θ+）﹣θ=，可得：T=2，

∵f（x0）=4，可得：sin（2ωx0﹣φ）=1，即f（x）關(guān)于x=x0對稱，而x=x0+1與x=x0的距離為半個周期，

∴sin[2ω（x0+1）﹣φ）=﹣1，

∴f（x0+1）=5sin[2ω（x0+1）﹣φ]﹣1=5×（﹣1）﹣1=﹣6．

故選：D．