【題目】已知函數
.
（1）若
在
上的最大值為
，求實數
的值；
（2）若對任意
，都有
恒成立，求實數
的取值范圍；
（3）在（1）的條件下，設
，對任意給定的正實數，曲線
上是否存在兩點
、
，使得
是以
（
為坐標原點）為直角頂點的直角三角形，且此三角形斜邊中點在
軸上？請說明理由。
【答案】（1）
（2）
（3）對任意給定的正實數
，曲線
上總存在兩點
，使得
是以
（
為坐標原點）為直角頂點的直角三角形，且此三角形斜邊中點在
軸上
【解析】
試題分析：（1）由
，得
，
令
，得
或
．
列表如下：
|
|
| 0 |
|
|
|
|
| 0 |
| 0 |
| |
|
|
| 極小值 |
| 極大值 |
|
∵
，
，
，
即最大值為
，
． 4分
（2）由
，得
．
，且等號不能同時取，
，
恒成立，即
．
令
，求導得，
，
當
時，
，從而
，
在
上為增函數，
，
． 8分
（3）由條件，
，
假設曲線
上存在兩點滿足題意，則只能在
軸兩側，
不妨設
，則
，且
．
是以（為坐標原點）為直角頂點的直角三角形，
，
， 10分
是否存在等價于方程
在
且時是否有解．
①若
時，方程
為
，化簡得
，
此方程無解； 11分
②若
時，
方程為
，即
，
設
，則
，
顯然，當
時，
，即
在
上為增函數，
的值域為
，即
，
當
時，方程
總有解．
對任意給定的正實數，曲線 上總存在兩點，使得
是以（為坐標原點）為直角頂點的直角三角形，且此三角形斜邊中點在軸上． 14分
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】用二分法研究函數f（x）=x3+3x﹣1的零點時，第一次經計算f（0）＜0，f（0.5）＞0，可得其中一個零點x0∈ ，第二次應計算的f（x）的值為f（ ）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經國務院批復同意，鄭州成功入圍國家中心城市，某校學生團針對“鄭州的發展環境”對20名學生進行問卷調查打分（滿分100分），得到如圖1所示莖葉圖.
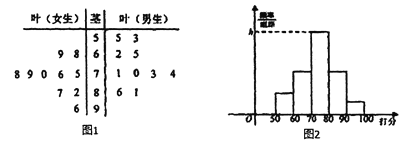
（1）分別計算男生女生打分的平均分，并用數學特征評價男女生打分的數據分布情況；
（2）如圖2按照打分區間
繪制的直方圖中，求最高矩形的高；
（3）從打分在70分以下（不含70分）的同學中抽取3人，求有女生被抽中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，若Ω是長方體ABCD﹣A1B1C1D1被平面EFGH截去幾何體EFGHB1C1后得到的幾何體，其中E為線段A1B1上異于B1的點，F為線段BB1上異于B1的點，且EH∥A1D1 ， 則下列結論中不正確的是（ ）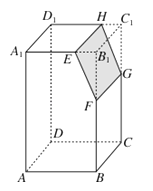
A.EH∥FG
B.四邊形EFGH是矩形
C.Ω是棱柱
D.Ω是棱臺
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD﹣A1B1C1D1中，M、N分別為棱C1D1、C1C的中點，有以下四個結論：
①直線AM與CC1是相交直線；
②直線AM與BN是平行直線；
③直線BN與MB1是異面直線；
④直線AM與DD1是異面直線．
其中正確的結論為 （注：把你認為正確的結論的序號都填上）．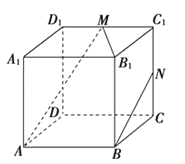
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD中，底面ABCD為正方形，PD⊥平面ABCD，PD=AB，E，F，G，H分別為PC、PD、BC、PA的中點．
求證：（1）PA∥平面EFG；
（2）DH⊥平面EFG．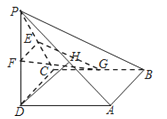
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，分別是橢圓
的左、右焦點.
（1）若點
是第一象限內橢圓上的一點， 
,求點
的坐標；
（2）設過定點
的直線
與橢圓交于不同的兩點
，且
為銳角（其中
為坐標原點），求直線
的斜率
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】矩形
的兩條對角線相交于點
， 
邊所在的直線的方程為
，點
在邊
所在的直線上．
（1）求邊
所在直線的方程；
（2）求矩形
外接圓的方程；
（3）過點
的直線
被矩形
的外接圓截得的弦長為
，求直線
的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C經過點
，且圓心
在直線
上，又直線
與圓C交于P,Q兩點.
（1）求圓C的方程；
（2）若
，求實數
的值；
(3)過點
作直線
，且
交圓C于M,N兩點，求四邊形
的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
