Question

2013年9月20日是第25個全國愛牙日。某區衛生部門成立了調查小組，調查 “常吃零食與患齲齒的關系”，對該區六年級800名學生進行檢查，按患齲齒和不患齲齒分類，得匯總數據：不常吃零食且不患齲齒的學生有60名，常吃零食但不患齲齒的學生有100名，不常吃零食但患齲齒的學生有140名.
（1）能否在犯錯概率不超過0.001的前提下，認為該區學生的常吃零食與患齲齒有關系？
（2）4名區衛生部門的工作人員隨機分成兩組，每組2人，一組負責數據收集，另一組負責數據處理.求工作人員甲分到負責收集數據組，工作人員乙分到負責數據處理組的概率.

	0.010	0.005	0.001
	6.635	7.879	10.828

附：

Answer 1

(1)學生常吃零食與患齲齒有關系(2)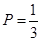

解析試題分析：(1)根據題意建立相應的列聯表,根據公式計算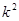,查表比較大小即可判斷是否有關
(2)古典概型,對四名工作人員編號，利用樹狀圖或者表格的方式列出四選兩個的所有基本事件,求出符合“工作人員甲分到負責收集數據組，工作人員乙分到負責數據處理組”的基本事件數,根據古典概型概率的計算公式即可得到相應的概率.
試題解析：（1）由題意可得列聯表：

	不常吃零食	常吃零食	總計
不患齲齒	60	100	160
患齲齒	140	500	640
總計	200	600	800

因為。
所以能在犯錯率不超過0.001的前提下,為該區學生常吃零食與患齲齒有關系。
（2）設其他工作人員為丙和丁，4人分組的所有情況如下表

<output id="2iqhv"></output>

小組	1	2	3	4	5	6
收集數據	甲乙	甲丙	甲丁	乙丙	乙丁	丙丁
處理數據	丙丁