
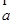 =(cosα,sinα),
=(cosα,sinα),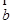 =(cosβ,sinβ),
=(cosβ,sinβ),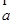 與
與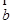 之間有關系|k
之間有關系|k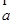 +
+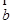 |=
|=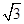 |
|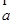 -k
-k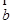 |,其中k>0,(Ⅰ)用k表示
|,其中k>0,(Ⅰ)用k表示 ;
;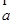 ·
·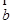 的最小值,并求此時
的最小值,并求此時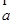 與
與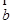 的夾角的大小。
的夾角的大小。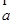 ·
·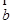
 ;(Ⅱ)
;(Ⅱ)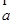 ·
·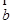 的最小值為
的最小值為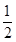 ,
,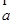 與
與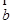 的夾角的大小60°.
的夾角的大小60°. ,可由已知
,可由已知 ,
,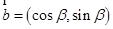 ,可得
,可得 ,結合|k
,結合|k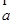 +
+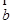 |=
|=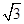 |
|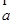 -k
-k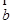 |,像這種與向量的模有關,可采用兩邊平方法,這樣兩邊平后可得
|,像這種與向量的模有關,可采用兩邊平方法,這樣兩邊平后可得 ,整理后可用k表示
,整理后可用k表示 ,(Ⅱ)求
,(Ⅱ)求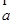 ·
·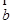 的最小值,由(Ⅰ)中函數的解析式,利用基本不等式,即可求出
的最小值,由(Ⅰ)中函數的解析式,利用基本不等式,即可求出 的最小值,利用最小值代入向量夾角公式,從而可得此時
的最小值,利用最小值代入向量夾角公式,從而可得此時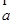 與
與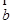 的夾角
的夾角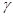 的大小.
的大小.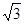 |a-kb|,兩邊平方,得|ka+b|2=(
|a-kb|,兩邊平方,得|ka+b|2=(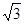 |a-kb|)2
|a-kb|)2 ∵a=(cosα,sinα),b=(cosβ,sinβ),
∵a=(cosα,sinα),b=(cosβ,sinβ), =
=
 ≥
≥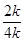 =
= ∴a·b的最小值為
∴a·b的最小值為 ,又∵a·b ="|" a|·|b |·cos
,又∵a·b ="|" a|·|b |·cos ,|a|=|b|=1∴
,|a|=|b|=1∴ =1×1×cos
=1×1×cos 。∴
。∴ =60°,此時a與b的夾角為60°。
=60°,此時a與b的夾角為60°。

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com