
【題目】如圖,已知四棱錐P﹣ABCD,PD⊥底面ABCD,且底面ABCD是邊長為2的正方形,M、N分別為PB、PC的中點. 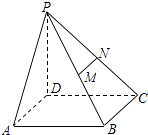
(1)證明:MN∥平面PAD;
(2)若PA與平面ABCD所成的角為45°,求四棱錐P﹣ABCD的體積V.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上, ![]() ,
, ![]() ,過
,過![]() 與坐標軸不垂直的直線
與坐標軸不垂直的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中點為
的中點為![]() ,在線段
,在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求實數
?若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種“籠具”由內,外兩層組成,無下底面,內層和外層分別是一個圓錐和圓柱,其中圓柱與圓錐的底面周長相等,圓柱有上底面,制作時需要將圓錐的頂端剪去,剪去部分和接頭忽略不計,已知圓柱的底面周長為![]() ,高為
,高為![]() ,圓錐的母線長為
,圓錐的母線長為![]() .
.
(1)求這種“籠具”的體積;
(2)現要使用一種紗網材料制作50個“籠具”,該材料的造價為每平方米8元,共需多少元?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].
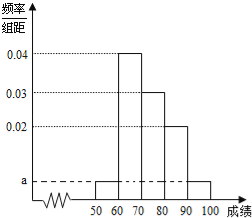
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如表所示,求數學成績在[50,90)之外的人數.
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在D上的函數,若存在區間[m,n]D及正實數k,使函數f(x)在[m,n]上的值域恰為[km,kn],則稱函數f(x)是k型函數.給出下列說法:
①f(x)=3﹣ ![]() 不可能是k型函數;
不可能是k型函數;
②若函數f(x)= ![]() (a≠0)是1型函數,則n﹣m的最大值為
(a≠0)是1型函數,則n﹣m的最大值為 ![]() ;
;
③若函數f(x)=﹣ ![]() x2+x是3型函數,則m=﹣4,n=0.
x2+x是3型函數,則m=﹣4,n=0.
其中正確說法個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
(1)求![]() 的軌跡
的軌跡![]()
(2)過軌跡![]() 上任意一點
上任意一點![]() 作圓
作圓![]() 的切線
的切線![]() ,設直線
,設直線![]() 的斜率分別是
的斜率分別是![]() ,試問在三個斜率都存在且不為0的條件下,
,試問在三個斜率都存在且不為0的條件下,  是否是定值,請說明理由,并加以證明.
是否是定值,請說明理由,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() .
.
(1)若f(x)>k的解集為{x|x<﹣3或x>﹣2},求k的值;
(2)若對任意x>0,f(x)≤t恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系.已知點
軸的正半軸為極軸,建立極坐標系.已知點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為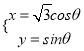 (
(![]() 為參數)
為參數)
(1)求點![]() 的直角坐標;化曲線
的直角坐標;化曲線![]() 的參數方程為普通方程;
的參數方程為普通方程;
(2)設![]() 為曲線
為曲線![]() 上一動點,以
上一動點,以![]() 為對角線的矩形
為對角線的矩形![]() 的一邊垂直于極軸,求矩形
的一邊垂直于極軸,求矩形![]() 周長的最小值,及此時
周長的最小值,及此時![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(x+ ![]() )+cosx,x∈R,
)+cosx,x∈R,
(1)求函數f(x)的最大值,并寫出當f(x)取得最大值時x的取值集合;
(2)若α∈(0, ![]() ),f(α+
),f(α+ ![]() )=
)= ![]() ,求f(2α)的值.
,求f(2α)的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com