
【題目】已知函數![]() ,
,![]()
(1)求函數![]() 的單調遞減區間;
的單調遞減區間;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不等的根,求實數
上有兩個不等的根,求實數![]() 的取值范圍;
的取值范圍;
(3)若存在![]() ,當
,當![]() 時,恒有
時,恒有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
試題分析:(1)由題已知函數![]() ,求函數的單調區間,可按照先求導,再令
,求函數的單調區間,可按照先求導,再令![]() ,又解出對應的不等式的解集,可得;(注意定義域優先)
,又解出對應的不等式的解集,可得;(注意定義域優先)
(2)由![]() 在區間上有兩個根,可通過構造函數
在區間上有兩個根,可通過構造函數![]() ,轉而利用導數考察函數的單調性和極值,再結合零點判定定理可建立關于
,轉而利用導數考察函數的單調性和極值,再結合零點判定定理可建立關于![]() 不等式組,可求。
不等式組,可求。
(3)由![]() ,都有
,都有![]() 為恒成立問題,可構造函數
為恒成立問題,可構造函數![]() ,又
,又![]() ,只需函數
,只需函數![]() 在給定的區間上單調遞增即可,可利用導數,讓導函數再區間上恒大于零可解出
在給定的區間上單調遞增即可,可利用導數,讓導函數再區間上恒大于零可解出![]() 的取值范圍.
的取值范圍.
試題解析:解:(1)因為函數![]() 的定義域為
的定義域為![]() ,
,
且![]() ,
,
令![]() ,即
,即![]() 解之得
解之得![]() :
:
所以函數![]() 的單調遞減區間為
的單調遞減區間為![]()
(2)令![]() ,
,
且定義域為![]()
所以![]() ,令
,令![]() ,
,![]() ,
,
列表如下:
|
| 1 |
|
| + | 0 | - |
| 遞增 | 極大值 | 遞減 |
所以函數![]() 在區間
在區間![]() 先單調遞減后單調遞增,故要使
先單調遞減后單調遞增,故要使![]() 有兩個不等的根,
有兩個不等的根,
只須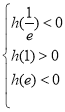 即
即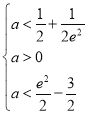 所以
所以![]()
(3)令![]() ,且
,且![]()
要使存在![]() ,當
,當![]() 時,恒有
時,恒有![]() ,
,
則只須![]() 即可,
即可,
也就是存在![]() ,當
,當![]() 時函數
時函數![]() 是單調遞增的,
是單調遞增的,
又因為![]() ,只須在
,只須在![]() 時
時![]() 成立,
成立,
即![]() ,解得
,解得![]() ,所以
,所以![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某中學將100名高二文科生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班進行教改實驗.為了了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”.
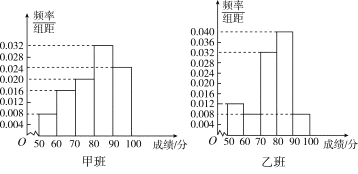
(Ⅰ)根據頻率分布直方圖填寫下面2×2列聯表;
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(Ⅱ)判斷能否在犯錯誤的概率不超過0.05的前提下認為:“成績優秀”與教學方式有關?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的極小值;
的極小值;
(Ⅱ)當![]() 時,過坐標原點
時,過坐標原點![]() 作曲線
作曲線![]() 的切線,設切點為
的切線,設切點為![]() ,求實數
,求實數![]() 的值;
的值;
(Ⅲ)設定義在![]() 上的函數
上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() :
: ![]() ,當
,當![]() 時,若
時,若![]() 在
在![]() 內恒成立,則稱
內恒成立,則稱![]() 為函數
為函數![]() 的“轉點”.當
的“轉點”.當![]() 時,試問函數
時,試問函數![]() 是否存在“轉點”.若存在,請求出“轉點”的橫坐標,若不存在,請說明理由.
是否存在“轉點”.若存在,請求出“轉點”的橫坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是
A. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都沒有公共點;
內的任意一條直線都沒有公共點;
B. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都平行;
內的任意一條直線都平行;
C. 若直線![]() 上有無數個點不在平面
上有無數個點不在平面 ![]() 內,則
內,則![]() ;
;
D. 如果兩條平行線中的一條與一個平面平行,那么另一條也與這個平面平行.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com