
【題目】已知在等比數(shù)列{an}中,a1=1,且a2是a1和a3﹣1的等差中項.
(1)求數(shù)列{an}的通項公式;
(2)若數(shù)列{bn}滿足bn=2n﹣1+an(n∈N*),求{bn}的前n項和Sn .
【答案】
(1)解:設(shè)等比數(shù)列{an}的公比為q,
∵a2是a1和a3﹣1的等差中項,a1=1,
∴2a2=a1+(a3﹣1)=a3,
∴ ![]() =2,
=2,
∴ ![]() =2n﹣1,(n∈N*).
=2n﹣1,(n∈N*).
(2)解:∵bn=2n﹣1+an,
∴ ![]() (2n﹣1+2n﹣1)
(2n﹣1+2n﹣1)
=[1+3+5+…+(2n﹣1)]+(1+2+22+…+2n﹣1)
= ![]() +
+ ![]()
=n2+2n﹣1.
【解析】(1)設(shè)等比數(shù)列{an}的公比為q,由a2是a1和a3﹣1的等差中項,a1=1,知2a2=a1+(a3﹣1)=a3 , 由此能求出數(shù)列{an}的通項公式..(2)由bn=2n﹣1+an , 知 ![]() (2n﹣1+2n﹣1)=[1+3+5+…+(2n﹣1)]+(1+2+22+…+2n﹣1),由等差數(shù)列和等比數(shù)列的求和公式能求出Sn .
(2n﹣1+2n﹣1)=[1+3+5+…+(2n﹣1)]+(1+2+22+…+2n﹣1),由等差數(shù)列和等比數(shù)列的求和公式能求出Sn .


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,F(xiàn)D⊥底面ABCD,M是AB的中點. 
(1)求證:平面CFM⊥平面BDF;
(2)點N在CE上,EC=2,F(xiàn)D=3,當(dāng)CN為何值時,MN∥平面BEF.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,將一半徑為2的半圓形紙板裁剪成等腰梯形ABCD的形狀,下底AB是半圓的直徑,上底CD的端點在圓周上,則所得梯形面積的最大值為( )
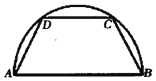
A. 3![]() B. 3
B. 3![]() C. 5
C. 5![]() D. 5
D. 5![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= 
(1)求函數(shù)f(x)的零點;
(2)若實數(shù)t滿足f(log2t)+f(log2 ![]() )<2f(2),求f(t)的取值范圍.
)<2f(2),求f(t)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如下圖所示的幾何體中, ![]() 為三棱柱,且
為三棱柱,且![]() ,四邊形
,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() .
.
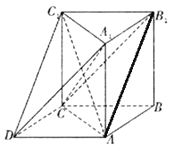
(1)求證: ![]() ;
;
(2)若![]() ,求證:
,求證: ![]() ;
;
(3)若![]() ,二面角
,二面角![]() 的余弦值為若
的余弦值為若![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四邊形ABCD中, ![]() =(2,﹣2),
=(2,﹣2), ![]() =(x,y),
=(x,y), ![]() =(1,
=(1, ![]() ).
).
(1)若 ![]() ∥
∥ ![]() ,求x,y之間的關(guān)系式;
,求x,y之間的關(guān)系式;
(2)滿足(1)的同時又有 ![]() ⊥
⊥ ![]() ,求x,y的值以及四邊形ABCD的面積.
,求x,y的值以及四邊形ABCD的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=lg(x2+tx+2)(t為常數(shù),且﹣2 ![]() <t<2
<t<2 ![]() ).
).
(1)當(dāng)x∈[0,2]時,求函數(shù)f(x)的最小值(用t表示);
(2)是否存在不同的實數(shù)a,b,使得f(a)=lga,f(b)=lgb,并且a,b∈(0,2).若存在,求出實數(shù)t的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() .?dāng)?shù)列
.?dāng)?shù)列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(2)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數(shù)![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差數(shù)列,若存在,求出所有滿足條件的
)成等差數(shù)列,若存在,求出所有滿足條件的![]() ,
,![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量 ![]() =(1,sinx),
=(1,sinx), ![]() =(cos(2x+
=(cos(2x+ ![]() ),sinx),函數(shù)f(x)=
),sinx),函數(shù)f(x)= ![]()
![]() ﹣
﹣ ![]() cos2x
cos2x
(1)求函數(shù)f(x)的解析式及其單調(diào)遞增區(qū)間;
(2)當(dāng)x∈[0, ![]() ]時,求函數(shù)f(x)的值域.
]時,求函數(shù)f(x)的值域.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com