【題目】如圖，
,
是經過小城
的東西方向與南北方向的兩條公路，小城
位于小城的東北方向，直線距離
.現規劃經過小城修建公路
(
,
分別在與上)，與,圍成三角形區域
.
(1)設
，
,求三角形區域周長的函數解析式
;
(2)現計劃開發周長最短的三角形區域，求該開發區域的面積.
【答案】（1） 
（2）開發區域
的面積為
【解析】分析：(1)先根據直角三角形求OA,OB,AB，再相加得三角形區域
周長的函數解析式; (2) 令
，化簡
，再根據三角函數有界性確定t范圍，解得
最小值，同時求出開發區域的面積.
詳解：解：（方法一）
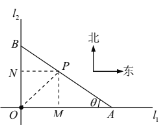
（1）如圖，過
分別作
、
的垂線，垂足分別為
、
，因為小城位于小城
的東北方向，且
，所以
，在
和
中，易得
，
，
所以
當
時，
，單調遞減
當
時，
，單調遞增
所以
時，取得最小值.
此時，
，
的面積
答：開發區域的面積為
（方法二）
（1）在
中，
，即
所以
在
中，
所以
（2）令，則
因為
，所以
，所以
由
，得
記 
因為
在
上單調遞減，所以當
時最小
此時
，即
，
所以
的面積
答：開發區域的面積為
科目：高中數學 來源： 題型：
【題目】甲、乙兩名同學參加一項射擊比賽游戲，其中任何一人每射擊一次擊中目標得2分，未擊中目標得0分．若甲、乙兩人射擊的命中率分別為 
和P，且甲、乙兩人各射擊一次得分之和為2的概率為 
．假設甲、乙兩人射擊互不影響，則P值為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）的定義域為R，且f（2）=2，又函數f（x）的導函數y=f′（x）的圖象如圖所示，若兩個正數a、b滿足f（2a+b）＜2，則 
的取值范圍是（ ）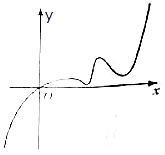 
A.（ 
，2）
B.（﹣∞， ）∪（2，+∞）
C.（2，+∞）
D.（﹣∞， ）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）是定義在（﹣∞，0）上的可導函數，其導函數為f′（x），且有xf′（x）＞x2+3f（x），則不等式8f（x+2014）+（x+2014）3f（﹣2）＞0的解集為（ ）
A.（﹣∞，﹣2016）
B.（﹣2018，﹣2016）
C.（﹣2018，0）
D.（﹣∞，﹣2018）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的圖象如圖所示（其中
是定義域為
的函數
的導函數），則以下說法錯誤的是（ ）．
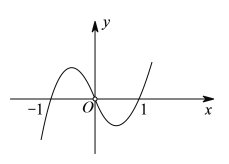
A. 
B. 當
時，函數取得極大值
C. 方程
與
均有三個實數根
D. 當
時，函數取得極小值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】辦公室裝修一新，放些植物花草可以清除異味，公司提供綠蘿、文竹、碧玉、蘆薈4種植物供員工選擇，每個員工任意選擇2種，則員工甲和乙選擇的植物全不同的概率為：
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
