
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是正方形,側棱
是正方形,側棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,過
的中點,過![]() 點作
點作![]() 交
交![]() 于點
于點![]() .
.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明: ![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案科目:高中數學 來源: 題型:
【題目】設U=R,A={x|x≤2,或x≥5},B= ![]() ,C={x|a<x<a+1}
,C={x|a<x<a+1}
(1)求A∪B和(UA)∩B
(2)若B∩C=C,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方形![]() 的邊長為
的邊長為![]() ,已知
,已知![]() ,將
,將![]() 沿
沿![]() 邊折起,折起后
邊折起,折起后![]() 點在平面
點在平面![]() 上的射影為
上的射影為![]() 點,則翻折后的幾何體中有如下描述:①
點,則翻折后的幾何體中有如下描述:①![]() 與
與![]() 所成角的正切值為
所成角的正切值為![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正確的命題序號為___________.
,其中正確的命題序號為___________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga ![]() (a>0且a≠1)是奇函數.
(a>0且a≠1)是奇函數.
(1)求實數m的值;
(2)判斷函數f(x)在區間(1,+∞)上的單調性并說明理由;
(3)當x∈(n,a﹣2)時,函數f(x)的值域為(1,+∞),求實數n,a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在實數集R中定義一種運算“*”,對任意給定的a,b∈R,a*b為唯一確定的實數,且具有性質: ⑴對任意a,b∈R,a*b=b*a;(2)對任意a∈R,a*0=a;(3)對任意a,b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.關于函數f(x)=(3x)* ![]() 的性質,有如下說法:
的性質,有如下說法:
①函數f(x)的最小值為3;
②函數f(x)為奇函數;
③函數f(x)的單調遞增區間為(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞).
,+∞).
其中所有正確說法的個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綜合題。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函數,且滿足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,側棱
,側棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]() 為
為![]() 中點.
中點.
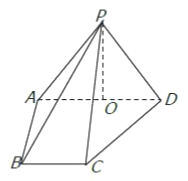
(1)求證: ![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)線段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距離為
的距離為![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx﹣4x,g(x)=﹣x2﹣3. (Ⅰ)求函數f(x)在x=1處的切線方程;
(Ⅱ)若存在x0∈[e,e2],使得f(x0)<g(x0)成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com