
(12分)已知動圓M過定點F(0,﹣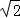 ),且與直線y=
),且與直線y=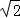 相切,橢圓N的對稱軸為坐標軸,一個焦點為F,點A(1,
相切,橢圓N的對稱軸為坐標軸,一個焦點為F,點A(1,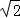 )在橢圓N上.
)在橢圓N上.
(1)求動圓圓心M的軌跡Γ的方程及橢圓N的方程;
(2)若動直線l與軌跡Γ在x=﹣4處的切線平行,且直線l與橢圓N交于B,C兩點,試求當△ABC面積取到最大值時直線l的方程.
(1)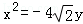 .
. ;(2)y=
;(2)y=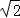 x±2.
x±2.
【解析】
試題分析:(1)由拋物線定義得,點M的軌跡是以F(0,﹣ )為焦點,直線y=
)為焦點,直線y= 為準線的拋物線,由此可得軌跡Γ的方程;設出橢圓方程,利用點A(1,
為準線的拋物線,由此可得軌跡Γ的方程;設出橢圓方程,利用點A(1, )在橢圓N上,可得橢圓N的方程;
)在橢圓N上,可得橢圓N的方程;
(2)設出切線方程,代入橢圓方程,求得|BC|,點A到直線的距離,表示出面積,利用基本不等式,即可求得△ABC面積取到最大值時直線l的方程.
【解析】
(1)過圓心M作直線y=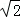 的垂線,垂足為H.
的垂線,垂足為H.
由題意得,|MH|=|MF|,由拋物線定義得,點M的軌跡是以F(0,﹣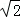 )為焦點,直線y=
)為焦點,直線y=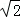 為準線的拋物線,
為準線的拋物線,
其方程為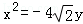 .
.
設橢圓方程為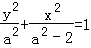 ,將點A代入方程
,將點A代入方程
整理得a4﹣5a2+4=0,解得a2=4或a2=1(舍去)
故所求的橢圓方程為 ;
;
(2)軌跡Γ的方程為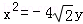 ,即
,即 ,則
,則 ,所以軌跡軌跡Γ在x=﹣4處的切線斜率為k=
,所以軌跡軌跡Γ在x=﹣4處的切線斜率為k= ,
,
設直線l方程為y= x+m,代入橢圓方程整理得4x2+2
x+m,代入橢圓方程整理得4x2+2 mx+m2﹣4=0
mx+m2﹣4=0
因為△=8m2﹣16(m2﹣4)>0,解得﹣2<m<2;
設B(x1,y1),C(x2,y2),則x1+x2=﹣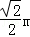 ,x1x2=
,x1x2=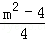
所以BC|= ×
× =
= ×
×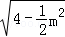
∵點A到直線的距離為d=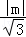 ,所以S△ABC=
,所以S△ABC= ×
×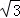 ×
×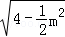 ×
×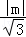 =
= ≤
≤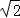
當且僅當 ,即m=±2時等號成立,此時直線l的方程為y=
,即m=±2時等號成立,此時直線l的方程為y=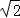 x±2.
x±2.


科目:高中數學 來源:[同步]2014年人教A版選修四4-1第一講1.1練習卷(解析版) 題型:選擇題
下列命題中正確的命題個數為( )
①如果一條直線與一平面平行,那么這條直線與平面內的任意直線平行;
②如果一條直線與一個平面相交,那么這條直線與這個平面內無數條直線垂直;
③過平面外一點有且只有一條直線與平面平行;
④一條直線上有兩點到一個平面的距離相等,則這條直線平行于這個平面.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:[同步]2014年人教A版選修一1-2第一章1.2練習卷(解析版) 題型:選擇題
(2014•珠海二模)通過隨機詢問100名性別不同的小學生是否愛吃零食,得到如下的列聯表:
| 男 | 女 | 總計 |
愛好 | 10 | 40 | 50 |
不愛好 | 20 | 30 | 50 |
總計 | 30 | 70 | 100 |
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 50.24 |
由K2=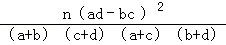 算得K2=
算得K2=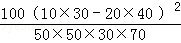 ≈4.762
≈4.762
參照附表,得到的正確結論( )
A.在犯錯誤的概率不超過5%的前提下,認為“是否愛吃零食與性別有關”
B.在犯錯誤的概率不超過5%的前提下,認為“是否愛吃零食與性別無關”
C.有97.5%以上的把握認為“是否愛吃零食與性別有關”
D.有97.5%以上的把握認為“是否愛吃零食與性別無關”
查看答案和解析>>
科目:高中數學 來源:[同步]2014年人教A版選修一1-2第一章1.1練習卷(解析版) 題型:選擇題
(2014•宜春模擬)在2013年9月15日,某市物價部門對本市的5家商場的某種商品的一天銷售量及其價格進行調查,5家商場的售價x元和銷售量y件之間的一組數據如下表所示:
價格x | 9 | 9.5 | 10 | 10.5 | 11 |
銷售量y | 11 | 10 | 8 | 6 | 5 |
由散點圖可知,銷售量y與價格x之間有較好的線性相關關系,其線性回歸方程是:y=﹣3.2x+a,則a=( )
A.﹣24 B.35.6 C.40.5 D.40
查看答案和解析>>
科目:高中數學 來源:[同步]2014年人教A版選修一1-2第一章1.1練習卷(解析版) 題型:選擇題
(2014•重慶)已知變量x與y正相關,且由觀測數據算得樣本平均數 =3,
=3,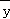 =3.5,則由該觀測數據算得的線性回歸方程可能是( )
=3.5,則由該觀測數據算得的線性回歸方程可能是( )
A.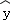 =0.4x+2.3 B.
=0.4x+2.3 B.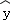 =2x﹣2.4 C.
=2x﹣2.4 C.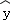 =﹣2x+9.5 D.
=﹣2x+9.5 D.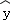 =﹣0.3x+4.4
=﹣0.3x+4.4
查看答案和解析>>
科目:高中數學 來源:[同步]2014年人教A版選修2-1 第二章圓錐曲線與方程練習卷(解析版) 題型:填空題
(5分)(2014•臺州一模)雙曲線x2﹣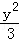 =1的兩條漸近線方程為 .
=1的兩條漸近線方程為 .
查看答案和解析>>
科目:高中數學 來源:[同步]2014年人教A版選修2-1 第二章圓錐曲線與方程練習卷(解析版) 題型:選擇題
(5分)已知橢圓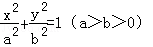 的左、右焦點分別為F1(﹣c,0),F2(c,0),若橢圓上存在點P使
的左、右焦點分別為F1(﹣c,0),F2(c,0),若橢圓上存在點P使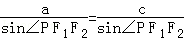 ,則該橢圓的離心率的取值范圍為( )
,則該橢圓的離心率的取值范圍為( )
A.(0, ) B.(
) B.(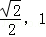 ) C.(0,
) C.(0,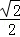 ) D.(
) D.( ,1)
,1)
查看答案和解析>>
科目:高中數學 來源:[同步]2014人教B版選修4-5 2.4最大值與最小值 優化數學模型(解析版) 題型:填空題
(2012•懷化二模)已知a+b+c=1,m=a2+b2+c2,則m的最小值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com