
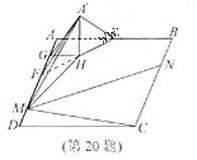
[番茄花園1] 如圖, 在矩形 中,點
中,點 分別
分別
在線段 上,
上,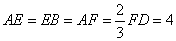 .沿直線
.沿直線
將  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)點 分別在線段
分別在線段 上,若沿直線
上,若沿直線 將四
將四
邊形 向上翻折,使
向上翻折,使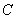 與
與 重合,求線段
重合,求線段
的長。
[番茄花園1]1.
[番茄花園1] 解析:本題主要考察空間點、線、面位置關系,二面角等基礎知識,空間向量的應用,同事考查空間想象能力和運算求解能力。
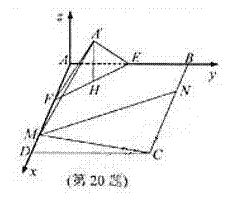 (Ⅰ)解:取線段EF的中點H,連結
(Ⅰ)解:取線段EF的中點H,連結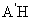 ,因為
,因為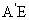 =
=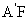 及H是EF的中點,所以
及H是EF的中點,所以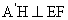 ,
,
又因為平面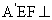 平面
平面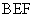 .
.
如圖建立空間直角坐標系A-xyz
則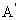 (2,2,
(2,2,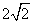 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故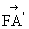 =(-2,2,2
=(-2,2,2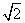 ),
),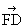 =(6,0,0).
=(6,0,0).
設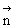 =(x,y,z)為平面
=(x,y,z)為平面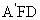 的一個法向量,
的一個法向量,
 -2x+2y+2
-2x+2y+2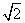 z=0
z=0
所以
6x=0.
取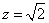 ,則
,則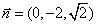 。
。
又平面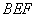 的一個法向量
的一個法向量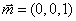 ,
,
故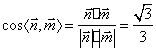 。
。
所以二面角的余弦值為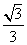
(Ⅱ)解:設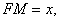 則
則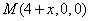 ,
,
因為翻折后,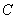 與
與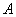 重合,所以
重合,所以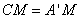 ,
,
故, 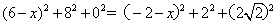 ,得
,得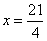 ,
,
經檢驗,此時點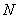 在線段
在線段 上,
上,
所以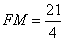 。
。
 方法二:
方法二:
(Ⅰ)解:取線段 的中點
的中點 ,
,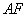 的中點
的中點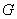 ,連結
,連結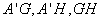 。
。
因為 =
=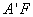 及
及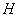 是
是 的中點,
的中點,
所以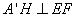
又因為平面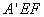
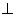 平面
平面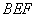 ,
,
所以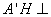 平面
平面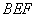 ,
,
又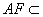 平面
平面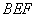 ,
,
故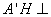
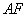 ,
,
又因為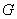 、
、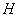 是
是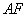 、
、 的中點,
的中點,
易知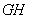 ∥
∥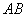 ,
,
所以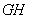
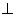
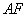 ,
,
于是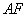
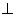 面
面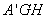 ,
,
所以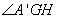 為二面角
為二面角 的平面角,
的平面角,
在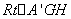 中,
中,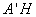 =
=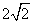 ,
,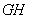 =2,
=2,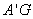 =
=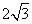
所以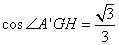 .
.
故二面角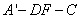 的余弦值為
的余弦值為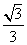 。
。
(Ⅱ)解:設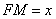 ,
,
因為翻折后,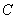 與
與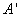 重合,
重合,
所以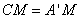 ,
,
而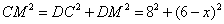 ,
,
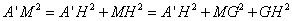
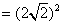
得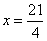 ,
,
經檢驗,此時點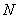 在線段
在線段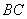 上,
上,
所以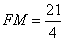 。
。
[番茄花園1]20.


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com