
【題目】如圖,某市新體育公園的中心廣場平面圖如圖所示,在y軸左側的觀光道曲線段是函數![]() ,
,![]() 時的圖象且最高點B(-1,4),在y軸右側的曲線段是以CO為直徑的半圓弧.
時的圖象且最高點B(-1,4),在y軸右側的曲線段是以CO為直徑的半圓弧.
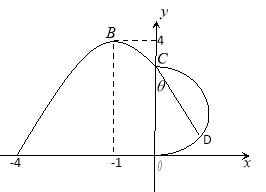
(1)試確定A,![]() 和
和![]() 的值;
的值;
(2)現要在右側的半圓中修建一條步行道CDO(單位:米),在點C與半圓弧上的一點D之間設計為直線段(造價為2萬元/米),從D到點O之間設計為沿半圓弧的弧形(造價為1萬元/米).設![]() (弧度),試用
(弧度),試用![]() 來表示修建步行道的造價預算,并求造價預算的最大值?(注:只考慮步行道的長度,不考慮步行道的寬度)
來表示修建步行道的造價預算,并求造價預算的最大值?(注:只考慮步行道的長度,不考慮步行道的寬度)
【答案】(1)![]() ;(2)造價
;(2)造價![]() ,
,![]() ,
,![]() 在
在![]() 時取極大值,也即造價預算最大值為(
時取極大值,也即造價預算最大值為(![]() )萬元.
)萬元.
【解析】
試題分析:(1)由“五點法”可求得![]() ;(2)由(1)求出
;(2)由(1)求出![]() 點坐標,得半圓的半徑,用
點坐標,得半圓的半徑,用![]() 表示出弦長
表示出弦長![]() 和弧長
和弧長![]() ,由題意可得造價
,由題意可得造價![]() ,
,![]() ,下面用導數的知識求出
,下面用導數的知識求出![]() 的最大值.
的最大值.
試題解析:(1)因為最高點B(-1,4),所以A=4;
![]() ,
,
因為![]()
代入點B(-1,4),
![]() ,
,
又![]() ;
;
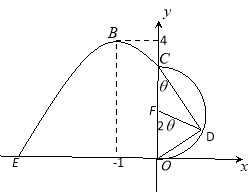
(2)由(1)可知:
![]() ,得點C
,得點C![]() 即
即![]() ,
,
取CO中點F,連結DF,因為弧CD為半圓弧,所以![]() ,
,
即![]() ,則圓弧段
,則圓弧段![]() 造價預算為
造價預算為![]() 萬元,
萬元,
![]() 中,
中,![]() ,則直線段CD造價預算為
,則直線段CD造價預算為![]() 萬元
萬元
所以步行道造價預算![]() ,
,![]() .
.
由![]() 得當
得當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞減
上單調遞減
所以![]() 在
在![]() 時取極大值,也即造價預算最大值為(
時取極大值,也即造價預算最大值為(![]() )萬元.……16分
)萬元.……16分


科目:高中數學 來源: 題型:
【題目】為了研究“教學方式”對教學質量的影響,某高中老師分別用兩種不同的教學方式對入學數學平均分數和優秀率都相同的甲、乙兩個高一新班進行教學(勤奮程度和自覺性都一樣).如圖莖葉圖為甲、乙兩班(每班均為20人)學生的數學期末考試成績.
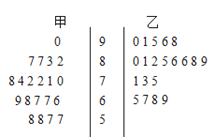
(1)現從甲班數學成績不低于80分的同學中隨機抽取兩名同學,求成績為87分的同學至少有一名被抽中的概率;
(2)學校規定:成績不低于75分的為優秀,請填寫![]() 列聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
列聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
甲班 | 乙班 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
參考公式與臨界值表: 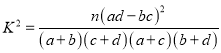 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生的學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
積極參加班級工作 | 不太主動參加班級工作 | 合計 | |
學習積極性高 | 18 | 7 | 25 |
學習積極性一般 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機抽查這個班的一名學生,那么抽到積極參加班級工作的學生的概率是多少?抽到不太主動參加班級工作且學習積極性一般的學生的概率是多少?
(2)試運用獨立性檢驗的思想方法分析:學生的學習積極性與對待班級工作的態度是否有關?并說明理由.
參考公式與臨界值表:K2=![]() .
.
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某集團為了獲得更大的收益,每年要投入一定的資金用于廣告促銷.經調查投入廣告費t(百萬元),可增加銷售額約為-t2+5t(百萬元)(0≤t≤5) (注:收益=銷售額-投放).
(1)若該公司將當年的廣告費控制在3百萬元之內,則應投入多少廣告費,才能使該公司由此獲得的收益最大?
(2)現該公司準備共投入3百萬元,分別用于廣告促銷和技術改造.經預測,每投入技術改造費x(百萬元),可增加的銷售額約為-![]() x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C:ρsin2θ=2acos θ(a>0),過點P(-2,-4)的直線l: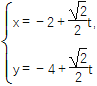 (t為參數)與曲線C相交于M,N兩點.
(t為參數)與曲線C相交于M,N兩點.
(1)求曲線C的直角坐標方程和直線l的普通方程;
(2)若|PM|,|MN|,|PN|成等比數列,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心為原點
的中心為原點![]() ,離心率
,離心率![]() ,其中一個焦點的坐標為
,其中一個焦點的坐標為![]()
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)當點![]() 在橢圓
在橢圓![]() 上運動時,設動點
上運動時,設動點![]() 的運動軌跡為
的運動軌跡為![]() 若點
若點![]() 滿足:
滿足: ![]() 其中
其中![]() 是
是![]() 上的點.直線
上的點.直線![]() 的斜率之積為
的斜率之積為![]() ,試說明:是否存在兩個定點
,試說明:是否存在兩個定點![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com