Question

【題目】高鐵、網購、移動支付和共享單車被譽為中國的“新四大發明”，彰顯出中國式創新的強勁活力.某移動支付公司從我市移動支付用戶中隨機抽取100名進行調查，得到如下數據：

每周移動支付次數	1次	2次	3次	4次	5次	6次及以上	總計
男	10	8	7	3	2	15	45
女	5	4	6	4	6	30	55
總計	15	12	13	7	8	45	100

（1）把每周使用移動支付超過3次的用戶稱為“移動支付活躍用戶”，能否在犯錯誤概率不超過0.005的前提下，認為是否為“移動支付活躍用戶”與性別有關？

（2）把每周使用移動支付6次及6次以上的用戶稱為“移動支付達人”，視頻率為概率，在我市所有“移動支付達人”中，隨機抽取4名用戶.

①求抽取的4名用戶中，既有男“移動支付達人”又有女“移動支付達人”的概率；

②為了鼓勵男性用戶使用移動支付，對抽出的男“移動支付達人”每人獎勵300元，記獎勵總金額為X，求X的分布列及均值.

附公式及表如下：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	2.072	2.076	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）在犯錯誤概率不超過0.005的前提下，能認為是否為“移動支付活躍用戶”與性別有關. （2）①②答案見解析.

【解析】

（1）由題意完成列聯表，結合列聯表計算可得，即可求得答案；

（2）視頻率為概率，在我市“移動支付達人”中，隨機抽取1名用戶，該用戶為男“移動支付達人”的概率為，女“移動支付達人”的概率為，結合已知，即可求得答案.

（1）由表格數據可得列聯表如下：

	非移動支付活躍用戶	移動支付活躍用戶	合計
男	25	20	45
女	15	40	55
合計	40	60	100

將列聯表中的數據代入公式計算得：

.

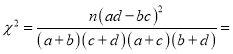
所以在犯錯誤概率不超過的前提下，能認為是否為“移動支付活躍用戶”與性別有關.

（2）視頻率為概率，在我市“移動支付達人”中，隨機抽取1名用戶，

該用戶為男“移動支付達人”的概率為，女“移動支付達人”的概率為.

①抽取的4名用戶中，既有男“移動支付達人”，又有女“移動支付達人”的概率為.

②記抽出的男“移動支付達人”人數為，則.

由題意得，

；

；

；

；

.

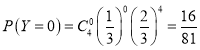所以的分布列為

	0	1	2	3	4

所以的分布列為

	0	300	600	900	1200

由，得的數學期望元.