
【題目】在海岸A處,發現北偏東45°方向,距A處( ![]() ﹣1)海里的B處有一艘走私船,在A處北偏西75°方向,距A處2海里的C處的緝私船奉命以10
﹣1)海里的B處有一艘走私船,在A處北偏西75°方向,距A處2海里的C處的緝私船奉命以10 ![]() 海里/小時的速度追截走私船,此時走私船正以10海里/小時的速度從B處向北偏東30°的方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間.
海里/小時的速度追截走私船,此時走私船正以10海里/小時的速度從B處向北偏東30°的方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間. 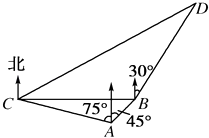
【答案】解:如圖所示,設緝私船追上走私船需t小時, 則有CD= ![]() ,BD=10t.在△ABC中,
,BD=10t.在△ABC中,
∵AB= ![]() ﹣1,AC=2,
﹣1,AC=2,
∠BAC=45°+75°=120°.
根據余弦定理可求得BC= ![]() .
.
∠CBD=90°+30°=120°.
在△BCD中,根據正弦定理可得
sin∠BCD= ![]() ,
,
∵∠CBD=120°,∴∠BCD=30°,∠BDC=30°,
∴BD=BC= ![]() ,則有
,則有
10t= ![]() ,t=
,t= ![]() =0.245(小時)=14.7(分鐘).
=0.245(小時)=14.7(分鐘).
所以緝私船沿北偏東60°方向,需14.7分鐘才能追上走私船.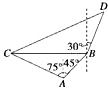
【解析】設緝私船追上走私船需t小時,進而可表示出CD和BD,進而在△ABC中利用余弦定理求得BC,進而在△BCD中,根據正弦定理可求得sin∠BCD的值,進而求得∠BDC=∠BCD=30°進而求得BD,進而利用BD=10t求得t.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)求函數![]() 的極值;
的極值;
(2)若![]() 時,函數
時,函數![]() 有且只有一個零點,求實數
有且只有一個零點,求實數![]() 的值;
的值;
(3若![]() ,對于區間
,對于區間![]() 上的任意兩個不相等的實數
上的任意兩個不相等的實數![]() ,都有
,都有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),P是平面內的一個動點,直線PA與PB交于點P,且它們的斜率之積是﹣
,0),P是平面內的一個動點,直線PA與PB交于點P,且它們的斜率之積是﹣ ![]() .
.
(1)求動點P的軌跡C的方程;
(2)設直線l:y=kx+1與曲線C交于M、N兩點,當線段MN的中點在直線x+2y=0上時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 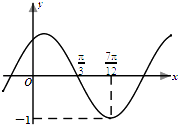
(1)求函數y=f(x)的解析式;
(2)求函數y=f(x)的單調增區間;
(3)求方程f(x)=0的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.
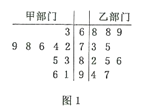
(1)若公司決定測試成績高于85分的員工獲得“職業技能好能手”稱號,求從這20名員工中任選三人,其中恰有兩人獲得“職業技能好能手”的概率;
(2)公司結合這次測試成績對員工的績效獎金進行調整(績效獎金方案如下表),若以甲部門這10人的樣本數據來估計該部門總體數據,且以頻率估計概率,從甲部門所有員工中任選3名員工,記績效獎金不小于![]() 的人數為
的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com