【題目】已知函數f（x）=（log2x）2﹣4log2x+1．
（1）求f（8）的值；
（2）當2≤x≤16時，求f（x）的最大值和最小值．
科目：高中數學 來源： 題型：
【題目】已知各項均為整數的數列{an}滿足an2≤1，1≤a12+a22+…+an2≤m，m，n∈N* ．
（1）若m=1，n=2，寫出所有滿足條件的數列{an}；
（2）設滿足條件的{an}的個數為f（n，m）．
①求f（2，2）和f（2016，2016）；
②若f（m+1，m）＞2016，試求m的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某險種的基本保費為
（單位：元），繼續購買該險種的投保人稱為續保人，
續保人本年度的保費與其上年度出險次數的關聯如下：
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 |
|
|
|
|
|
|
隨機調查了該險種的400名續保人在一年內的出險情況，得到如下統計表：
出險次數 | 0 | 1 | 2 | 3 | 4 |
|
頻數 | 120 | 100 | 60 | 60 | 40 | 20 |
（Ⅰ）記A為事件：“一續保人本年度的保費不高于基本保費”.求
的估計值；
（Ⅱ）記B為事件：“一續保人本年度的保費高于基本保費但不高于基本保費的190％”.
求
的估計值；
（III）求續保人本年度的平均保費估計值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“累積凈化量
”是空氣凈化器質量的一個重要衡量指標，它是指空氣凈化從開始使用到凈化效率為50%時對顆粒物的累積凈化量，以克表示，根據
《空氣凈化器》國家標準，對空氣凈化器的累計凈化量有如下等級劃分：
累積凈化量（克） |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器（共5000臺）的質量，隨機抽取
臺機器作為樣本進行估計，已知這臺機器的累積凈化量都分布在區間
中，按照
、
、
、
、
均勻分組，其中累積凈化量在的所有數據有：4.5,4.6,5.2,5.3,5.7和5.9，并繪制了頻率分布直方圖，如圖所示：
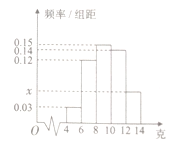
（1）求的值及頻率分布直方圖中
的值；
（2）以樣本估計總體，試估計這批空氣凈化器（共5000臺）中等級為
的空氣凈化器有多少臺？
（3）從累積凈化量在的樣本中隨機抽取2臺，求恰好有1臺等級為的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】解答
（1）集合M={1，2，（m2﹣3m﹣1）+（m2﹣5m﹣6）i}，N={3，﹣1}，M∩N={3}，求實數m的值．
（2）已知12= 
×1×2×3，12+22= ×2×3×5，12+22+32= ×3×4×7，12+22+32+42= ×4×5×9，由此猜想12+22+…+n2（n∈N*）的表達式并用數學歸納法證明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f（x）定義域中任意的x1 ， x2（x1≠x2），有如下結論：
①f（x1+x2）=f（x1）f（x2）；
②f（x1x2）=f（x1）+f（x2）；
③ 
＞0；
④ 
．
當f（x）=lgx時，上述結論中正確結論的序號是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=x2﹣16x+q+3：
（1）若函數在區間[﹣1，1]上存在零點，求實數q的取值范圍；
（2）問：是否存在常數t（t≥0），當x∈[t，10]時，f（x）的值域為區間D，且D的長度為12﹣t．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A（﹣4，4）、B（4，4），直線AM與BM相交于點M，且直線AM的斜率與直線BM的斜率之差為﹣2，點M的軌跡為曲線C．
（1）求曲線C 的軌跡方程；
（2）Q為直線y=﹣1上的動點，過Q做曲線C的切線，切點分別為D、E，求△QDE的面積S的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
