
【題目】點![]() 到點
到點![]() ,
, ![]() 及到直線
及到直線![]() 的距離都相等,如果這樣的點恰好只有一個,那么實數
的距離都相等,如果這樣的點恰好只有一個,那么實數![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
【答案】D
【解析】試題分析:由題意知![]() 在拋物線
在拋物線![]() 上,設
上,設 ,則有
,則有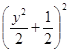
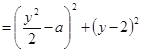 ,化簡得
,化簡得![]() ,當
,當![]() 時,符合題意;當
時,符合題意;當![]() 時,
時,![]() ,有
,有![]() ,
,![]() ,則
,則![]() ,所以選D.
,所以選D.
考點:1、點到直線的距離公式;2、拋物線的性質.
【方法點睛】本題考查拋物線的概念、性質以及數形結合思想,屬于中檔題,到點![]() 和直線
和直線![]() 的距離相等,則
的距離相等,則![]() 的軌跡是拋物線,再由直線與拋物線的位置關系可求;拋物線的定義是解決物線問題的基礎,它能將兩種距離(拋物線上的點到到焦點的距離、拋物線上的點到準線的距離)進行等量轉化,如果問題中涉及拋物線的焦點和準線,又能與距離聯系起來,那么用拋物線的定義就能解決.
的軌跡是拋物線,再由直線與拋物線的位置關系可求;拋物線的定義是解決物線問題的基礎,它能將兩種距離(拋物線上的點到到焦點的距離、拋物線上的點到準線的距離)進行等量轉化,如果問題中涉及拋物線的焦點和準線,又能與距離聯系起來,那么用拋物線的定義就能解決.
【題型】單選題
【結束】
13
【題目】在極坐標系中,已知兩點![]() ,
, ![]() ,則
,則![]() ,
, ![]() 兩點間的距離為__________.
兩點間的距離為__________.
科目:高中數學 來源: 題型:
【題目】某動物園要為剛入園的小動物建造一間兩面靠墻的三角形露天活動室,地面形狀如圖所示,已知已有兩面墻的夾角為![]() ,墻
,墻![]() 的長度為
的長度為![]() 米,(已有兩面墻的可利用長度足夠大),記
米,(已有兩面墻的可利用長度足夠大),記![]() .
.
(1)若![]() ,求
,求![]() 的周長(結果精確到0.01米);
的周長(結果精確到0.01米);
(2)為了使小動物能健康成長,要求所建的三角形露天活動室面積,![]() 的面積盡可能大,當
的面積盡可能大,當![]() 為何值時,該活動室面積最大?并求出最大面積.
為何值時,該活動室面積最大?并求出最大面積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,動點![]() 到兩點
到兩點![]() 的距離之和等于4,設點
的距離之和等于4,設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 交于
交于![]() 兩點.
兩點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)![]() 的面積是否存在最大值,若存在,求出
的面積是否存在最大值,若存在,求出![]() 的面積的最大值;若不存在,說明理由.
的面積的最大值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“![]() ”是“對任意的正數
”是“對任意的正數![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分也不必要條件
【答案】A
【解析】分析:根據基本不等式,我們可以判斷出“![]() ”?“對任意的正數x,2x+
”?“對任意的正數x,2x+![]() ≥1”與“對任意的正數x,2x+
≥1”與“對任意的正數x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,進而根據充要條件的定義,即可得到結論.
解答:解:當“a=![]() ”時,由基本不等式可得:
”時,由基本不等式可得:
“對任意的正數x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“對任意的正數x,2x+
”?“對任意的正數x,2x+![]() ≥1”為真命題;
≥1”為真命題;
而“對任意的正數x,2x+![]() ≥1的”時,可得“a≥
≥1的”時,可得“a≥![]() ”
”
即“對任意的正數x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”為假命題;
”為假命題;
故“a=![]() ”是“對任意的正數x,2x+
”是“對任意的正數x,2x+![]() ≥1的”充分不必要條件
≥1的”充分不必要條件
故選A
【題型】單選題
【結束】
11
【題目】如圖,四棱錐![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]()
![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() ,則平面
,則平面![]() 與平面
與平面![]() 的夾角的余弦值為( )
的夾角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了弘揚民族文化,某校舉行了“我愛國學,傳誦經典”考試,并從中隨機抽取了100名考生的成績(得分均為整數,滿足100分)進行統計制表,其中成績不低于80分的考生被評為優秀生,請根據頻率分布表中所提供的數據,用頻率估計概率,回答下列問題.
分組 | 頻數 | 頻率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合計 | 100 | 1.00 |
(1)求![]() 的值并估計這100名考生成績的平均分;
的值并估計這100名考生成績的平均分;
(2)按頻率分布表中的成績分組,采用分層抽樣抽取20人參加學校的“我愛國學”宣傳活動,求其中優秀生的人數;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為檢測空氣質量,某市環保局隨機抽取了甲、乙兩地2016年20天的PM2.5日平均濃度(單位:微克/立方米)是監測數據,得到甲地PM2.5日平均濃度的頻率分布直方圖和乙地PM2.5日平均濃度的頻數分布表.
甲地20天PM2.5日平均濃度頻率分布直方圖

乙地20天PM2.5日平均濃度頻數分布表

(1)根據乙地20天PM2.5日平均濃度的頻數分布表作出相應的頻率分布直方圖,并通過兩個頻率分布直方圖比較兩地PM2.5日平均濃度的平均值及分散程度;(不要求計算出具體值,給出結論即可)
(2)求甲地20天PM2.5日平均濃度的中位數;
(3)通過調查,該市市民對空氣質量的滿意度從高到低分為三個等級:

記事件![]() :“甲地市民對空氣質量的滿意度等級為不滿意”。根據所給數據,利用樣本估計總體的統計思想,以事件發生的頻率作為相應事件發生的概率,求事件
:“甲地市民對空氣質量的滿意度等級為不滿意”。根據所給數據,利用樣本估計總體的統計思想,以事件發生的頻率作為相應事件發生的概率,求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com