
(13分)(2011•重慶)設函數f(x)=sinxcosx﹣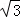 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函數y=f(x)的圖象按 =(
=( ,
,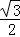 )平移后得到的函數y=g(x)的圖象,求y=g(x)在(0,
)平移后得到的函數y=g(x)的圖象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
(I)π(II)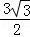
解析試題分析:(I)先利用誘導公式,二倍角公式與和角公式將函數解析式化簡整理,然后利用周期公式可求得函數的最小正周期.
(II)由(I)得函數y=f(x),利用函數圖象的變換可得函數y=g(x)的解析式,通過探討角的范圍,即可的函數g(x)的最大值.
解:(I)∵f(x)=sinxcosx﹣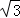 cos(x+π)cosx
cos(x+π)cosx
=sinxcosx+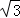 cosxcosx
cosxcosx
=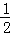 sin2x+
sin2x+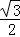 cos2x+
cos2x+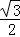
=sin(2x+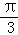 )+
)+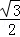
∴f(x)的最小正周期T=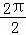 =π
=π
(II)∵函數y=f(x)的圖象按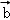 =(
=(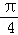 ,
,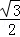 )平移后得到的函數y=g(x)的圖象,
)平移后得到的函數y=g(x)的圖象,
∴g(x)=sin(2x+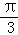 ﹣
﹣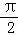 )+
)+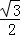 +
+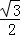 =sin(2x﹣
=sin(2x﹣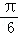 )+
)+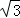
∵0<x≤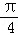 ∴
∴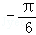 <2x﹣
<2x﹣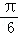 ≤
≤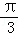 ,
,
∴y=g(x)在(0,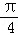 ]上的最大值為:
]上的最大值為: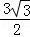 .
.
點評:本題考查了三角函數的周期及其求法,函數圖象的變換及三角函數的最值,各公式的熟練應用是解決問題的根本,體現了整體意識,是個中檔題.


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知向量 ,
, ,設函數
,設函數 ,且
,且 的圖象過點
的圖象過點 和點
和點 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)將 的圖象向左平移
的圖象向左平移 (
( )個單位后得到函數
)個單位后得到函數 的圖象.若
的圖象.若 的圖象上各最高點到點
的圖象上各最高點到點 的距離的最小值為1,求
的距離的最小值為1,求 的單調增區間.
的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正三角形ABC的邊長為2,D,E,F分別在三邊AB,BC和CA上,且D為AB的中點, ,
,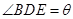 ,
,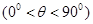 .
.
(1)當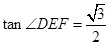 時,求
時,求 的大小;
的大小;
(2)求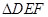 的面積S的最小值及使得S取最小值時
的面積S的最小值及使得S取最小值時 的值.
的值.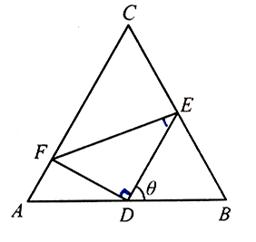
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com