
【題目】公元2222年,有一種高危傳染病在全球范圍內(nèi)蔓延,被感染者的潛伏期可以長達(dá)10年,期間會有約0.05%的概率傳染給他人,一旦發(fā)病三天內(nèi)即死亡,某城市總?cè)丝诩s200萬人,專家分析其中約有1000名傳染者,為了防止疾病繼續(xù)擴(kuò)散,疾病預(yù)防控制中心現(xiàn)決定對全市人口進(jìn)行血液檢測以篩選出被感染者,由于檢測試劑十分昂貴且數(shù)量有限,需要將血樣混合后一起檢測以節(jié)約試劑,已知感染者的檢測結(jié)果為陽性,末被感染者為陰性,另外檢測結(jié)果為陽性的血樣與檢測結(jié)果為陰性的血樣混合后檢測結(jié)果為陽性,同一檢測結(jié)果的血樣混合后結(jié)果不發(fā)生改變.
(1)若對全市人口進(jìn)行平均分組,同一分組的血樣將被混合到一起檢測,若發(fā)現(xiàn)結(jié)果為陽性, 則再在該分組內(nèi)逐個檢測排査,設(shè)每個組![]() 個人,那么最壞情況下,需要進(jìn)行多少次檢測可以找到所有的被感染者?在當(dāng)前方案下,若要使檢測的次數(shù)盡可能少,每個分組的最優(yōu)人數(shù)?
個人,那么最壞情況下,需要進(jìn)行多少次檢測可以找到所有的被感染者?在當(dāng)前方案下,若要使檢測的次數(shù)盡可能少,每個分組的最優(yōu)人數(shù)?
(2)在(1)的檢測方案中,對于檢測結(jié)果為陽性的組來取逐一檢測排査的方法并不是很好, 或可將這些組的血樣再進(jìn)行一次分組混合血樣檢測,然后再進(jìn)行逐一排査,仍然考慮最壞的情況,請問兩次要如何分組,使檢測總次數(shù)盡可能少?
(3)在(2)的檢測方案中,進(jìn)行了兩次分組混合血樣檢測,仍然考慮最壞情況,若再進(jìn)行若干次分組混合血樣檢測,是否會使檢測次數(shù)更少?請給出最優(yōu)的檢測方案.
【答案】(1)![]() 次,45人;(2)第一次每組159人,第二次每組13人;(3)見解析
次,45人;(2)第一次每組159人,第二次每組13人;(3)見解析
【解析】
(1)根據(jù)最壞的情況是1000名被感染者分布在其中1000組里,可得檢測總次數(shù),再用基本不等式可得;
(2)設(shè)第一次每個組![]() 人,第二次每個組
人,第二次每個組![]() 人,可得檢測總次數(shù),再用三元基本不等式,結(jié)合整數(shù)解可得;
人,可得檢測總次數(shù),再用三元基本不等式,結(jié)合整數(shù)解可得;
(3)設(shè)第![]() 次分組中,每組人數(shù)為
次分組中,每組人數(shù)為![]() ,則可得檢測總次數(shù),然后運用
,則可得檢測總次數(shù),然后運用![]() 元基本不等式,結(jié)合
元基本不等式,結(jié)合![]() ,可得
,可得![]() 的最小值,進(jìn)而得到所求結(jié)果.
的最小值,進(jìn)而得到所求結(jié)果.
(1)200萬人平均分組,每組![]() 人,總共分
人,總共分![]() 組,每組檢測一次,共需檢測
組,每組檢測一次,共需檢測![]() 次,最壞的情況是1000名被感染者分布在其中1000組里,每組一人,然后在這1000組里逐個排查,每組需檢測
次,最壞的情況是1000名被感染者分布在其中1000組里,每組一人,然后在這1000組里逐個排查,每組需檢測![]() 次,共需檢測1000
次,共需檢測1000![]() 次,所以找到所有的被感染者共需檢測
次,所以找到所有的被感染者共需檢測![]()
![]() 次,
次,
由![]()
![]()
![]()
![]() ,
,
當(dāng)且僅當(dāng)![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
![]()
![]() 時等號成立.
時等號成立.
由于![]() 為正整數(shù),
為正整數(shù),
所以當(dāng)![]() 時,
時,![]()
![]() ,
,
當(dāng)![]() 時,
時,![]()
![]() ,
,
因為![]() ,
,
所以要使檢測總次數(shù)盡可能少,每個分組的最優(yōu)人數(shù)為45人.
(2)設(shè)第一次每個組![]() 人,分
人,分![]() 組;第二次每個組
組;第二次每個組![]() 人,分
人,分![]() 組
組
第一次需檢測![]() 次,由(1)的思路知,第二次共需檢測
次,由(1)的思路知,第二次共需檢測![]()
![]() 次,
次,
所以兩次檢測的總次數(shù)為![]()
![]()
![]() ,
,
因為![]()
![]()
![]()
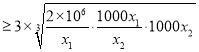
![]()
![]() ,
,
當(dāng)且僅當(dāng)![]() ,
,
即![]() ,
,![]() ,
,![]() 時等號成立,
時等號成立,
因為![]()
![]() ,
,![]()
![]() ,且
,且![]() 為正整數(shù),
為正整數(shù),
且![]() ,
,![]() ,
,
所以![]() ,時兩次檢測的總次數(shù)盡可能少,
,時兩次檢測的總次數(shù)盡可能少,
則第一次每個組159人,第二次每個組13人,可使檢測總次數(shù)盡可能少.
(3)假設(shè)進(jìn)行![]() 次這樣的分組檢測,可以達(dá)到檢測次數(shù)更少,
次這樣的分組檢測,可以達(dá)到檢測次數(shù)更少,
設(shè)第![]() 次分組中,每組人數(shù)為
次分組中,每組人數(shù)為![]() ,
,
則總共檢測次數(shù)為![]() ,
,
因為![]()
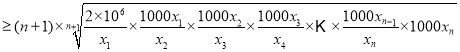
![]() ,
,
當(dāng)且僅當(dāng)![]() ,時等號成立,
,時等號成立,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
當(dāng)![]() 時,
時,![]()
![]()
![]() ,
,
因為![]() ,且
,且![]() 為正整數(shù),
為正整數(shù),
所以可取![]() ,即這樣進(jìn)行了18次檢驗可得到總次數(shù)更小.
,即這樣進(jìn)行了18次檢驗可得到總次數(shù)更小.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() 相交于不同的
相交于不同的![]() 兩點.
兩點.
(1)如果直線![]() 過拋物線的焦點,求
過拋物線的焦點,求![]() 的值;
的值;
(2)如果![]()
![]() ,證明:直線
,證明:直線![]() 必過一定點,并求出該定點.
必過一定點,并求出該定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某位同學(xué)進(jìn)行社會實踐活動,為了對白天平均氣溫與某奶茶店的某種飲料銷量之間的關(guān)系進(jìn)行分析研究,他分別記錄了12月11日至12月15日的白天平均氣溫![]() (℃)與該小賣部的這種飲料銷量
(℃)與該小賣部的這種飲料銷量![]() (杯),得到如下數(shù)據(jù):
(杯),得到如下數(shù)據(jù):
日期 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
(1)請根據(jù)所給五組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)據(jù)(1)中所得的線性回歸方程,若天氣預(yù)報12月16日的白天平均氣溫7(℃),請預(yù)測該奶茶店這種飲料的銷量. (參考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 是極坐標(biāo)方程式
是極坐標(biāo)方程式![]() ,以極點為平面直角坐標(biāo)系的原點,極軸為
,以極點為平面直角坐標(biāo)系的原點,極軸為![]() 軸的正半軸,建立平面直角坐標(biāo)系,直線
軸的正半軸,建立平面直角坐標(biāo)系,直線![]() 是參數(shù)方程是
是參數(shù)方程是 (
(![]() 為參數(shù)).
為參數(shù)).
(1)求曲線![]() 的直角坐標(biāo)方程和直線
的直角坐標(biāo)方程和直線![]() 的普通方程;
的普通方程;
(2)設(shè)點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
按照某學(xué)者的理論,假設(shè)一個人生產(chǎn)某產(chǎn)品單件成本為![]() 元,如果他賣出該產(chǎn)品的單價為
元,如果他賣出該產(chǎn)品的單價為![]() 元,則他的滿意度為
元,則他的滿意度為![]() ;如果他買進(jìn)該產(chǎn)品的單價為
;如果他買進(jìn)該產(chǎn)品的單價為![]() 元,則他的滿意度為
元,則他的滿意度為![]() .如果一個人對兩種交易(賣出或買進(jìn))的滿意度分別為
.如果一個人對兩種交易(賣出或買進(jìn))的滿意度分別為![]() 和
和![]() ,則他對這兩種交易的綜合滿意度為
,則他對這兩種交易的綜合滿意度為![]() .
.
現(xiàn)假設(shè)甲生產(chǎn)A、B兩種產(chǎn)品的單件成本分別為12元和5元,乙生產(chǎn)A、B兩種產(chǎn)品的單件成本分別為3元和20元,設(shè)產(chǎn)品A、B的單價分別為![]() 元和
元和![]() 元,甲買進(jìn)A與賣出B的綜合滿意度為
元,甲買進(jìn)A與賣出B的綜合滿意度為![]() ,乙賣出A與買進(jìn)B的綜合滿意度為
,乙賣出A與買進(jìn)B的綜合滿意度為![]()
(1)求![]() 和
和![]() 關(guān)于
關(guān)于![]() 、
、![]() 的表達(dá)式;當(dāng)
的表達(dá)式;當(dāng)![]() 時,求證:
時,求證:![]() =
=![]() ;
;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 、
、![]() 分別為多少時,甲、乙兩人的綜合滿意度均最大?最大的綜合滿意度為多少?(3)記(2)中最大的綜合滿意度為
分別為多少時,甲、乙兩人的綜合滿意度均最大?最大的綜合滿意度為多少?(3)記(2)中最大的綜合滿意度為![]() ,試問能否適當(dāng)選取
,試問能否適當(dāng)選取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同時成立,但等號不同時成立?試說明理由。
同時成立,但等號不同時成立?試說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)設(shè)函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在定義域上為增函數(shù),求實數(shù)
在定義域上為增函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)在(Ⅰ)的條件下,若函數(shù)![]() ,
,![]() 使得
使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項和,已知
項和,已知![]() ,
, ![]() .
.
(Ⅰ)求數(shù)列![]() 的通項公式;
的通項公式;
(Ⅱ)令![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)![]() 的圖像與
的圖像與![]() 軸相交于點
軸相交于點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側(cè)),與
的左側(cè)),與![]() 軸相交于點
軸相交于點![]() ,連接
,連接![]() 、
、![]() .
.
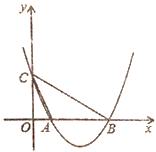
(1)求線段![]() 的長;
的長;
(2)若![]() 平分
平分![]() ,求
,求![]() 的值;
的值;
(3)該函數(shù)圖象的對稱軸上是否存在點![]() ,使得
,使得![]() 為等邊三角形?若存在,求出
為等邊三角形?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將正方形![]() 沿對角線
沿對角線![]() 折成直二面角
折成直二面角![]() ,有如下四個結(jié)論:
,有如下四個結(jié)論:
①![]() ;
;
②![]() 是等邊三角形;
是等邊三角形;
③![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ;
;
④![]() 與
與![]() 所成的角為
所成的角為![]() .
.
其中錯誤的結(jié)論是____________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com