
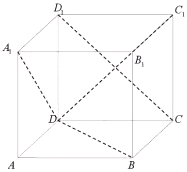
【題目】如圖,![]() 的棱長為1的正方體,任作平面
的棱長為1的正方體,任作平面![]() 與對角線
與對角線![]() 垂直,使得
垂直,使得![]() 與正方體的每個面都有公共點,這樣得到的截面多邊形的面積為
與正方體的每個面都有公共點,這樣得到的截面多邊形的面積為![]() ,周長為
,周長為![]() 的范圍分別是_____________(用集合表示)
的范圍分別是_____________(用集合表示)
【答案】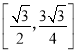 ;
;![]()
【解析】
由線面垂直的性質可知截面多邊形的邊與所在的正方形的對角線平行,利用相似比即可求得截面周長為定值.
連接![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]()
![]() ,又
,又![]()
![]() 平面
平面![]() ,
,![]()
同理可證![]()
則![]() 平面
平面![]() ,
,
設平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,
,
則![]() ,又
,又![]() ,
,
![]() ,
,
同理可得平面![]() 與其他各面的交線都與此平面的對角線平行,
與其他各面的交線都與此平面的對角線平行,
設![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,
同理可得六邊形其他相鄰兩邊的和為![]() ,
,
![]() 六邊形的周長
六邊形的周長![]() 為定值
為定值![]() .
.
因為截面與各面的交線與各面的對角線平行,所以不管六邊形如何變化,六邊形的每個內角都是![]() ,并且相鄰邊長的和為
,并且相鄰邊長的和為![]() ,通過構造邊長為
,通過構造邊長為![]() 的菱形,并且有一個角為
的菱形,并且有一個角為![]() ,
,
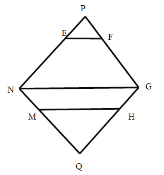
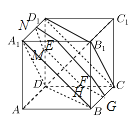
六邊形![]() 的面積是如圖兩個等邊三角形的面積減上下兩個等邊三角形的面積,
的面積是如圖兩個等邊三角形的面積減上下兩個等邊三角形的面積,![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,![]()
![]() ,
,
![]()
所以截面多邊形面積的取值范圍是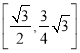
故答案為: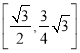 ;
;![]()


科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足條件
滿足條件![]() ,且
,且![]()
(1)計算![]() ,請猜測數列
,請猜測數列![]() 的通項公式,并用數學歸納法證明;
的通項公式,并用數學歸納法證明;
(2)請分別構造一個二階和三階行列式,使它們的值均為![]() ,其中,要求所構造的三階行列式主對角線下方的元素均為零,并用按某行或者某列展開的方法驗證三階行列式的值為
,其中,要求所構造的三階行列式主對角線下方的元素均為零,并用按某行或者某列展開的方法驗證三階行列式的值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A.“![]() ”是“
”是“![]() ”充分的條件;
”充分的條件;
B.“![]() ”是“
”是“![]() ”成立的充分不必要條件;
”成立的充分不必要條件;
C.命題“已知![]() ,
,![]() 是實數,若
是實數,若![]() ,則
,則![]() 或
或![]() ”為真命題;
”為真命題;
D.命題“若![]() ,
,![]() 都是正數,則
都是正數,則![]() 也是正數”的逆否命題是“若
也是正數”的逆否命題是“若![]() 不是正數,則
不是正數,則![]() ,
,![]() 都不是正數”.
都不是正數”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店為了了解銷售單價(單位:元)在![]() 內的圖書銷售情況,從2018年上半年已經銷售的圖書中隨機抽取100本,獲得的所有樣本數據按照
內的圖書銷售情況,從2018年上半年已經銷售的圖書中隨機抽取100本,獲得的所有樣本數據按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,制成如圖所示的頻率分布直方圖,已知樣本中銷售單價在
分成6組,制成如圖所示的頻率分布直方圖,已知樣本中銷售單價在![]() 內的圖書數是銷售單價在
內的圖書數是銷售單價在![]() 內的圖書數的2倍.
內的圖書數的2倍.
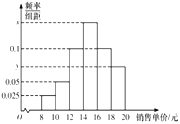
(1)求出x與y,再根據頻率分布直方圖佔計這100本圖書銷售單價的平均數、中位數(同一組中的數據用該組區間的中點值作代表);
(2)用分層抽樣的方法從銷售單價在![]() 內的圖書中共抽取40本,求單價在6組樣本數據中的圖書銷售的數量;
內的圖書中共抽取40本,求單價在6組樣本數據中的圖書銷售的數量;
(3)從(2)中抽取且價格低于12元的書中任取2本,求這2本書價格都不低于10元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖給出的是某高校土木工程系大四年級55名學生期末考試專業成績的頻率分布折線圖(連接頻率分布直方圖中各小長方形上端的中點),其中組距為10,且本次考試中最低分為50分,最高分為100分.根據圖中所提供的信息,則下列結論中正確的是( )

A. 成績是75分的人數有20人
B. 成績是100分的人數比成績是50分的人數多
C. 成績落在70-90分的人數有35人
D. 成績落在75-85分的人數有35人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐的側面展開圖是一個半圓.

(1)求圓錐的母線與底面所成的角;
(2)過底面中心![]() 且平行于母線
且平行于母線![]() 的截平面,若截面與圓錐側面的交線是焦參數(焦點到準線的距離)為
的截平面,若截面與圓錐側面的交線是焦參數(焦點到準線的距離)為![]() 的拋物線,求圓錐的全面積;
的拋物線,求圓錐的全面積;
(3)過底面點![]() 作垂直且于母線
作垂直且于母線![]() 的截面,若截面與圓錐側面的交線是長軸為
的截面,若截面與圓錐側面的交線是長軸為![]() 的橢圓,求橢圓的面積(橢圓號
的橢圓,求橢圓的面積(橢圓號![]() 的面積
的面積![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}為等比數列, ![]() 公比為
公比為![]()
![]() 為數列{an}的前n項和.
為數列{an}的前n項和.
(1)若![]() 求
求![]() ;
;
(2)若調換![]() 的順序后能構成一個等差數列,求
的順序后能構成一個等差數列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常數![]() ,使得對任意正整數n,不等式
,使得對任意正整數n,不等式![]() 總成立?若存在,求出
總成立?若存在,求出![]() 的范圍,若不存在,請說明理由.
的范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線x2=4y的焦點F和點A(-1,8),點P為拋物線上一點,則|PA|+|PF|的最小值為( )
A. 16 B. 6 C. 12 D. 9
查看答案和解析>>
科目:高中數學 來源: 題型:
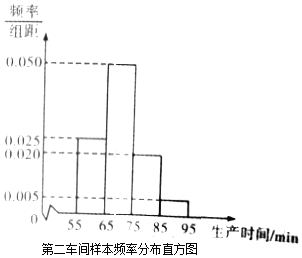
【題目】某工廠有兩個車間生產同一種產品,第一車間有工人200人,第二車間有工人400人,為比較兩個車間工人的生產效率,采用分層抽樣的方法抽取工人,并對他們中每位工人生產完成一件產品的時間(單位:min)分別進行統計,得到下列統計圖表(按照[55,65),[65,75),[75,85),[85,95]分組).
分組 | 頻數 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合計 | 20 |
第一車間樣本頻數分布表
(Ⅰ)分別估計兩個車間工人中,生產一件產品時間小于75min的人數;
(Ⅱ)分別估計兩車間工人生產時間的平均值,并推測哪個車間工人的生產效率更高?(同一組中的數據以這組數據所在區間中點的值作代表)
(Ⅲ)從第一車間被統計的生產時間小于75min的工人中,隨機抽取3人,記抽取的生產時間小于65min的工人人數為隨機變量X,求X的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com