
如圖,四棱錐 中,底面
中,底面 為平行四邊形,
為平行四邊形, ,
, ,
, ⊥底面
⊥底面 .
.
(1)證明:平面 平面
平面 ;
;
(2)若二面角 為
為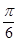 ,求
,求 與平面
與平面 所成角的正弦值.
所成角的正弦值.
(1)證明過程詳見解析;(2)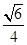 .
.
解析試題分析:(1)可以遵循思路面面垂直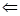 線面垂直
線面垂直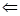 線線垂直,即證明面面垂直只需要證明其中一個面里面的一條直線垂直與另外一個面即可,即證明
線線垂直,即證明面面垂直只需要證明其中一個面里面的一條直線垂直與另外一個面即可,即證明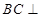 面PDB,線面垂直只需要證明BC與面內相交的兩條直線垂直即可,即
面PDB,線面垂直只需要證明BC與面內相交的兩條直線垂直即可,即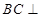 BD,
BD, 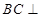 PD,前者可有三角形的勾股定理證得,后者由線面垂直得到
PD,前者可有三角形的勾股定理證得,后者由線面垂直得到
(2)求線面夾角可以利用三維空間直角坐標系,分別以DA,DB,PD三條兩兩垂直的直線建立坐標系,求面法向量與直線的夾角的余弦值的絕對值即為線面夾角的余弦值.
試題解析:
(1)∵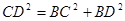 ∴
∴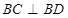
又∵ ⊥底面
⊥底面 ∴
∴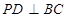
又∵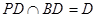 ∴
∴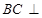 平面
平面
而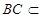 平面
平面 ∴平面
∴平面 平面
平面 5分
5分
(1)由(1)所證,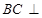 平面
平面 ,所以∠
,所以∠ 即為二面角P-BC-D的平面角,即∠
即為二面角P-BC-D的平面角,即∠
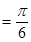
而 ,所以
,所以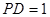 7分
7分
分別以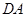 、
、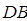 、
、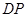 為
為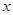 軸、
軸、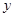 軸、
軸、 軸建立空間直角坐標系.則
軸建立空間直角坐標系.則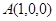 ,
,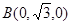 ,
,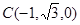 ,
, 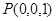 ,所以,
,所以,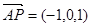 ,
,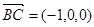 ,
,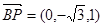 ,設平面
,設平面 的法向量為
的法向量為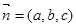 ,則
,則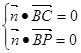 ,即
,即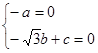 可解得
可解得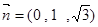 ∴
∴ 與平面
與平面 所成角的正弦值為
所成角的正弦值為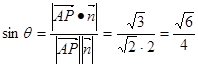 12分
12分
考點:面面垂直 線面夾角


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
如圖,A,B,C,D為空間四點.在△ABC中,AB=2,AC=BC=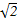 .等邊三角形ADB以AB為軸轉動.
.等邊三角形ADB以AB為軸轉動.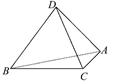
(1)當平面ADB⊥平面ABC時,求CD.
(2)當△ADB轉動時,是否總有AB⊥CD?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB是圓O的直徑,PA垂直圓O所在的平面,C是圓O上的點.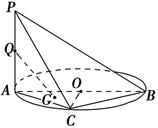
(1)求證:BC⊥平面PAC;
(2)設Q為PA的中點,G為△AOC的重心,求證:QG∥平面PBC.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱錐S—ABC中,SC⊥平面ABC,點P、M分別是SC和SB的中點,設PM=AC=1,∠ACB=90°,直線AM與直線SC所成的角為60°。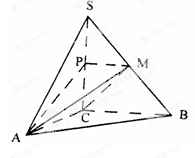
(1)求證:平面MAP⊥平面SAC。
(2)求二面角M—AC—B的平面角的正切值;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知 、
、 、
、 為不在同一直線上的三點,且
為不在同一直線上的三點,且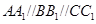 ,
,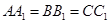 .
.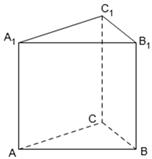
(1)求證:平面 //平面
//平面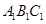 ;
;
(2)若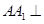 平面
平面 ,且
,且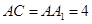 ,
,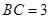 ,
,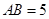 ,求證:
,求證: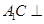 平面
平面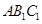 ;
;
(3)在(2)的條件下,求二面角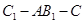 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com