
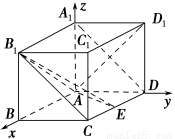
如圖,在長方體ABCD-A1B1C1D1中,AA1=AD=1,E為CD的中點.

(1)求證:B1E⊥AD1.
(2)在棱AA1上是否存在一點P,使得DP∥平面B1AE?若存在,求AP的長;若不存在,說明理由.
(3)若二面角A-B1E-A1的大小為30°,求AB的長.
(1)見解析(2)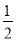 (3)2
(3)2
【解析】(1)以A為原點,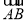 ,
,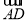 ,
,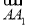 的方向分別為x軸、y軸、z軸的正方向建立空間直角坐標系(如圖).設AB=a,則A(0,0,0),D(0,1,0),D1(0,1,1),
的方向分別為x軸、y軸、z軸的正方向建立空間直角坐標系(如圖).設AB=a,則A(0,0,0),D(0,1,0),D1(0,1,1),
E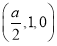 ,B1(a,0,1),
,B1(a,0,1),
故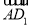 =(0,1,1),
=(0,1,1),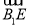 =
= ,
,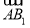 =(a,0,1),
=(a,0,1),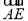 =
=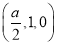 .
.
∵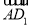 ·
·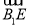 =-
=-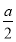 ×0+1×1+(-1)×1=0,
×0+1×1+(-1)×1=0,
∴B1E⊥AD1.
(2)假設在棱AA1上存在一點P(0,0,z0)(0≤z0≤1),
使得DP∥平面B1AE.此時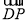 =(0,-1,z0).
=(0,-1,z0).
又設平面B1AE的法向量n=(x,y,z).
由n⊥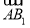 ,n⊥
,n⊥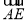 ,得
,得 .
.
取x=1,得平面B1AE的一個法向量n=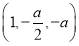
要使DP∥平面B1AE,只要n⊥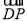 ,有
,有 -az0=0,
-az0=0,
解得z0=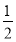 .
.
又DP?平面B1AE,
∴存在點P,滿足DP∥平面B1AE,此時AP=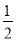 .
.
(3)連接A1D,B1C,由長方體ABCD-A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,
∴AD1⊥B1C.
又由(1)知B1E⊥AD1,且B1C∩B1E=B1,
∴AD1⊥平面DCB1A1,
∴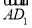 是平面A1B1E的一個法向量,此時
是平面A1B1E的一個法向量,此時 =(0,1,1).
=(0,1,1).
設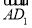 與n所成的角為θ,則
與n所成的角為θ,則
cos θ= =
= .
.
∵二面角A-B1E-A1的大小為30°,
∴|cos θ|=cos 30°,即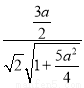 =
=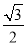 ,
,
解得a=2,即AB的長為.2


科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練選修4-1練習卷(解析版) 題型:填空題
如圖所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD∶BD=9∶4,則AC∶BC的值為________.

查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-6-3練習卷(解析版) 題型:填空題
設F為拋物線C:y2=4x的焦點,過點P(-1,0)的直線l交拋物線C于A、B兩點,點Q為線段AB的中點,若|FQ|=2,則直線l的斜率等于________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-6-2練習卷(解析版) 題型:選擇題
已知中心在原點的雙曲線C的右焦點為F(3,0),離心率等于 ,則C的方程是( ).
,則C的方程是( ).
A. =1 B.
=1 B. =1
=1
C.  =1 D.
=1 D.  =1
=1
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-6-1練習卷(解析版) 題型:選擇題
過點(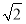 ,0)引直線l與曲線y=
,0)引直線l與曲線y=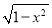 相交于A、B兩點,O為坐標原點,當△AOB的面積取最大值時,直線l的斜率等于( ).
相交于A、B兩點,O為坐標原點,當△AOB的面積取最大值時,直線l的斜率等于( ).

A.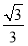 B.-
B.-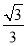 C.±
C.±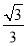 D.-
D.-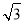
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-5-3練習卷(解析版) 題型:填空題
在正方體ABCD-A1B1C1D1中,M,N分別是棱CD,CC1的中點,則異面直線A1M與DN所成的角的大小是________

查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-5-2練習卷(解析版) 題型:解答題
在直角梯形ABCD中,AB∥CD,AD⊥AB,CD=2AB=4,AD= ,E為CD的中點,將△BCE沿BE折起,使得CO⊥DE,其中垂足O在線段DE內.
,E為CD的中點,將△BCE沿BE折起,使得CO⊥DE,其中垂足O在線段DE內.

(1)求證:CO⊥平面ABED;
(2)問∠CEO(記為θ)多大時,三棱錐C-AOE的體積最大,最大值為多少.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-5-1練習卷(解析版) 題型:選擇題
已知矩形ABCD的面積為8,當矩形ABCD周長最小時,沿對角線AC把
△ACD折起,則三棱錐D-ABC外接的球表面積等于( ).
A.8π B.16π C.48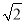 π D.不確定的實數
π D.不確定的實數
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪專題復習知能提升演練1-3-1練習卷(解析版) 題型:填空題
已知α∈R,sin α+2cos α= ,則tan 2α等于________.
,則tan 2α等于________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com