
【題目】已知函數![]() (
(![]() ,且
,且![]() )在
)在![]() 上單調遞增,且關于
上單調遞增,且關于![]() 的方程
的方程![]() 恰有兩個不相等的實數解,則
恰有兩個不相等的實數解,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由題意首先求得a的取值范圍,然后結合函數的解析式將原問題轉化為兩函數圖像存在兩個交點的問題,數形結合即可確定a的取值范圍.
由函數的解析式可知函數在區間![]() 上單調遞增,
上單調遞增,
當![]() 時,函數
時,函數![]() 單調遞減,由復合函數的單調性法則可知:
單調遞減,由復合函數的單調性法則可知:![]() ,
,
且函數在![]() 處滿足:
處滿足:![]() ,解得:
,解得:![]() ,故
,故![]() ,
,
方程![]() 恰有兩個不相等的實數解,則函數
恰有兩個不相等的實數解,則函數![]() 與函數
與函數![]() 的圖像有且僅有兩個不同的交點,
的圖像有且僅有兩個不同的交點,
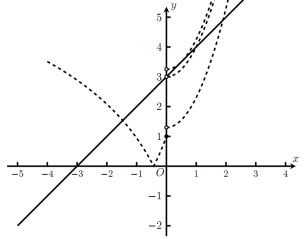
繪制函數![]() 的圖像如圖中虛線所示,
的圖像如圖中虛線所示,
令![]() 可得:
可得:![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,
則直線![]() 與函數
與函數![]() 的圖像在區間
的圖像在區間![]() 上存在唯一的交點,
上存在唯一的交點,
原問題轉化為函數![]() 與二次函數
與二次函數![]() 在區間
在區間![]() 上存在唯一的交點,
上存在唯一的交點,
很明顯當![]() ,即
,即![]() 時滿足題意,
時滿足題意,
當直線與二次函數相切時,設切點坐標為![]() ,亦即
,亦即![]() ,
,
由函數的解析式可得:![]() ,故:
,故:![]() ,則
,則![]() ,
,
切點坐標為![]() ,從而:
,從而:![]() ,即
,即![]() .
.
據此可得:![]() 的取值范圍是
的取值范圍是![]() .
.
故選:D.


科目:高中數學 來源: 題型:
【題目】某企業準備投入適當的廣告費對甲產品進行促銷宣傳,在一年內預計銷量![]() (萬件)與廣告費
(萬件)與廣告費![]() (萬元)之間的函數關系為
(萬元)之間的函數關系為![]() ,已知生產此產品的年固定投入為
,已知生產此產品的年固定投入為![]() 萬元,每生產1萬件此產品仍需要再投入30萬元,且能全部銷售完,若每件甲產品銷售價格(元)定為:“平均每件甲產品生產成本的150%”與“年平均每件產品所占廣告費的50%”之和,則當廣告費為1萬元時,該企業甲產品的年利潤比不投入廣告費時的年利潤增加了__________萬元.
萬元,每生產1萬件此產品仍需要再投入30萬元,且能全部銷售完,若每件甲產品銷售價格(元)定為:“平均每件甲產品生產成本的150%”與“年平均每件產品所占廣告費的50%”之和,則當廣告費為1萬元時,該企業甲產品的年利潤比不投入廣告費時的年利潤增加了__________萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() ,若不等式
,若不等式![]() 的解集為(1,4),且方程f(x)=x有兩個相等的實數根。
的解集為(1,4),且方程f(x)=x有兩個相等的實數根。
(1)求f(x)的解析式;
(2)若不等式f(x)>mx在![]() 上恒成立,求實數m的取值范圍;
上恒成立,求實數m的取值范圍;
(3)解不等式![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點M(0,-2)、N(3,1),且圓心C在直線x+2y+1=0上.
(1)求圓C的方程;
(2)設直線ax-y+1=0與圓C交于A,B兩點,是否存在實數a,使得過點P(2,0)的直線l垂直平分弦AB?若存在,求出實數a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題10分) 從3名男生和![]() 名女生中任選2人參加比賽。
名女生中任選2人參加比賽。
①求所選2人都是男生的概率;
②求所選2人恰有1名女生的概率;
③求所選2人中至少有1名女生的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1,且E,F分別是BC,B1C1中點.

(1)求證:A1B∥平面AEC1;
(2)求直線AF與平面AEC1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{![]() }的前n項和為Sn,
}的前n項和為Sn,![]() ,且對任意的n∈N*,n≥2都有
,且對任意的n∈N*,n≥2都有![]() 。
。
(1)若![]() 0,
0,![]() ,求r的值;
,求r的值;
(2)數列{![]() }能否是等比數列?說明理由;
}能否是等比數列?說明理由;
(3)當r=1時,求證:數列{![]() }是等差數列。
}是等差數列。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com