
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為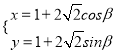 (
(![]() 為參數),在極坐標系中,直線
為參數),在極坐標系中,直線![]() 的方程為:
的方程為: ![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)寫出曲線![]() 的直角坐標方程,并指出它是何種曲線;
的直角坐標方程,并指出它是何種曲線;
(Ⅱ)設![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,
兩點, ![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
科目:高中數學 來源: 題型:
【題目】【2017湖南婁底二模】如圖,四棱錐![]() 的底面
的底面![]() 是平行四邊形,側面
是平行四邊形,側面![]() 是邊長為2的正三角形,
是邊長為2的正三角形, ![]()
![]() ,
, ![]() .
.
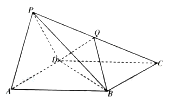
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)設![]() 是棱
是棱![]() 上的點,當
上的點,當![]() 平面
平面![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=Asin(ωx+φ)在一個周期內的圖象如圖,此函數的解析式為( ) 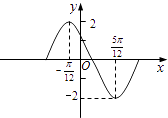
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,平面四邊形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四點F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求證:平面CBE⊥平面EDB;
(Ⅲ)當x=2時,求二面角F﹣EB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(
=( ![]() ,cos
,cos ![]() ),
), ![]() =(cos
=(cos ![]() ,1),且f(x)=
,1),且f(x)= ![]()
![]() .
.
(1)求函數f(x)的最小正周期;
(2)求函數f(x)在區間[﹣π,π]上的最大值和最小值及取得最值時x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )滿足
)滿足 ![]() =2,且
=2,且 ![]() 與
與 ![]() ﹣
﹣ ![]() 的夾角為120° , t∈R,則|(1﹣t)
的夾角為120° , t∈R,則|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 滿足(
滿足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,則
|=3,則 ![]()
![]() 的最大值為 .
的最大值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,直線l1的參數方程為![]() (t為參數),直線l2的參數方程為
(t為參數),直線l2的參數方程為 .設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
.設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
(1)寫出C的普通方程;
(2)以坐標原點為極點,x軸正半軸為極軸建立極坐標系,設l3:ρ(cosθ+sinθ) ![]() =0,M為l3與C的交點,求M的極徑.
=0,M為l3與C的交點,求M的極徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com