
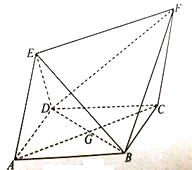
【題目】如圖,四邊形 ![]() 為菱形,四邊形
為菱形,四邊形 ![]() 為平行四邊形,設
為平行四邊形,設 ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,
, ![]() .
.
(1)證明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,求三棱錐
,求三棱錐 ![]() 的體積.
的體積.
【答案】
(1)
解:證明:連接 ![]() ,
,
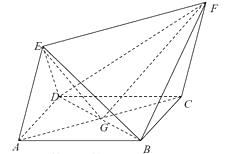
∵四邊形 ![]() 為菱形,
為菱形,
∵ ![]() ,
,
在 ![]() 和
和 ![]() 中,
中,
![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]() ;
;
(2)
解法一:連接 ![]() ,∵
,∵ ![]() 面
面 ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
在平行四邊形 ![]() 中,易知
中,易知 ![]() ,
,
∴ ![]() ,即
,即 ![]() ,又因為
,又因為 ![]() 為平面
為平面 ![]() 內的兩條相交直線,所以
內的兩條相交直線,所以 ![]() 平面
平面 ![]() ,所以點
,所以點 ![]() 到平面
到平面 ![]() 的距離為
的距離為 ![]() ,
,
∵ ![]() ,
,
∴三棱錐 ![]() 的體積為
的體積為 ![]() .
.
解法二:∵ ![]() ,∴點
,∴點 ![]() 到平面
到平面 ![]() 的距離為點
的距離為點 ![]() 到平面
到平面 ![]() 的距離的兩倍,所以
的距離的兩倍,所以 ![]() ,
,
作 ![]() ,∵平面
,∵平面 ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
,
∴三棱錐 ![]() 的體積為
的體積為 ![]() .
.
【解析】(1)做輔助線,連接EG,通過證明△EAD和△EAB全等,得到ED=EB,即EG⊥BD。四邊形ABCD為菱形,則有AC⊥BD,故BD⊥平面ACFE,進而可以證明兩個平面垂直。(2)連接FG,證明FG為點F到△BDE的距離,求出△BDE的面積,通過三棱錐公式即可求出三棱錐體積。


科目:高中數學 來源: 題型:
【題目】已知圓O1:(x﹣2)2+y2=16和圓O2:x2+y2=r2(0<r<2),動圓M與圓O1、圓O2都相切,切圓圓心M的軌跡為兩個橢圓,這兩個橢圓的離心率分別為e1 , e2(e1>e2),則e1+2e2的最小值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來篷布發展的新機遇,2015年雙11期間,某購物平臺的銷售業績高達918億人民幣.與此同時,相關管理部門推出了針對電商的商品和服務的評價體系.現從評價系統中選出200次成功交易,并對其評價進行統計,對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)是否可以在犯錯誤概率不超過0.1%的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的5次購物中,設對商品和服務全好評的次數為隨機變量X: ①求對商品和服務全好評的次數X的分布列(概率用組合數算式表示);
②求X的數學期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F1、F2是雙曲線C: ![]() =1(a>0,b>0)的左、右焦點,O為坐標原點,點P在雙曲線C的右支上,且滿足|F1F2|=2|OP|,|PF1|≥3|PF2|,則雙曲線C的離心率的取值范圍為( )
=1(a>0,b>0)的左、右焦點,O為坐標原點,點P在雙曲線C的右支上,且滿足|F1F2|=2|OP|,|PF1|≥3|PF2|,則雙曲線C的離心率的取值范圍為( )
A.(1,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.(1, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xe2x﹣lnx﹣ax.
(1)當a=0時,求函數f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范圍;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的兩條漸近線與拋物線y2=2px(p>0)的準線分別交于O、A、B三點,O為坐標原點.若雙曲線的離心率為2,△AOB的面積為
=1(a>0,b>0)的兩條漸近線與拋物線y2=2px(p>0)的準線分別交于O、A、B三點,O為坐標原點.若雙曲線的離心率為2,△AOB的面積為 ![]() ,則p=( )
,則p=( )
A.1
B.![]()
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P( ![]() ,1)和橢圓C:
,1)和橢圓C: ![]() +
+ ![]() =1.
=1.
(1)設橢圓的兩個焦點分別為F1 , F2 , 試求△PF1F2的周長及橢圓的離心率;
(2)若直線l: ![]() x﹣2y+m=0(m≠0)與橢圓C交于兩個不同的點A,B,設直線PA與PB的斜率分別為k1 , k2 , 求證:k1+k2=0.
x﹣2y+m=0(m≠0)與橢圓C交于兩個不同的點A,B,設直線PA與PB的斜率分別為k1 , k2 , 求證:k1+k2=0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 經過點M(﹣2,﹣1),離心率為
經過點M(﹣2,﹣1),離心率為 ![]() .過點M作傾斜角互補的兩條直線分別與橢圓C交于異于M的另外兩點P、Q. (I)求橢圓C的方程;
.過點M作傾斜角互補的兩條直線分別與橢圓C交于異于M的另外兩點P、Q. (I)求橢圓C的方程;
(II)試判斷直線PQ的斜率是否為定值,證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣a(x﹣1),g(x)=ex(Ⅰ)若函數f(x)在區間(0,9]為增函數,求實數a的取值范圍;
(Ⅱ)當a≠0時,過原點分別作曲線y=f(x)與y=g(x)的切線l1 , l2 , 已知兩切線的斜率互為倒數,證明: ![]() <a<
<a< ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com