
【題目】已知平面上兩定點M(0,﹣2)、N(0,2),P為一動點,滿足![]()
![]() |
|![]() ||
||![]() |
|
(I)求動點P的軌跡C的方程;
(II)若A、B是軌跡C上的兩不同動點,且![]() λ
λ![]() .分別以A、B為切點作軌跡C的切線,設(shè)其交點Q,證明
.分別以A、B為切點作軌跡C的切線,設(shè)其交點Q,證明![]() 為定值.
為定值.
【答案】(I)x2=8y
(II)見解析
【解析】
(I)先設(shè)P(x,y),求動點P的軌跡C的方程,即尋找x,y之間的關(guān)系,結(jié)合向量的坐標(biāo)運算即可得到.
(II)先設(shè)出A,B兩點的坐標(biāo),利用向量關(guān)系及向量運算法則,用A,B的坐標(biāo)表示出![]() ,最后看其是不是定值即可.
,最后看其是不是定值即可.
(I)設(shè)P(x,y).
由已知 ![]() (x,y+2),
(x,y+2),![]() (0,4),
(0,4),![]() (﹣x,2﹣y),
(﹣x,2﹣y),
![]()
![]() 4y+8.
4y+8.
|![]() ||
||![]() |=4
|=4![]()
∵![]()
![]() |
|![]() ||
||![]() |
|
∴4y+8=4![]() 整理,得x2=8y
整理,得x2=8y
即動點P的軌跡C為拋物線,其方程為x2=8y.
(II)由已知N(0,2).
即得(﹣x1,2﹣y1)=λ(x2,y2﹣2)
設(shè)A(x1,y1),B(x2,y2).由![]() λ
λ![]()
即得(﹣x1,2﹣y1)=λ(x2,y2﹣2),
∴﹣x1=λx2…(1),
2﹣y1=λ(y2﹣2)…(2)
將(1)式兩邊平方并把x12=8y1,x2/span>2=8y2代入得y1=![]() y2
y2
解得 y1=2λ,y2![]() ,
,
且有x1x2=﹣λx22=﹣8λy2=﹣16.
拋物線方程為 y=![]() ,求導(dǎo)得y′
,求導(dǎo)得y′![]() x.
x.
所以過拋物線上A、B兩點的切線方程分別是 y![]() x1(x﹣x1)+y1,y
x1(x﹣x1)+y1,y![]() x2(x﹣x2)+y2,
x2(x﹣x2)+y2,
即y![]() x1x
x1x![]() x12,y
x12,y![]() x2x
x2x![]() x22
x22
解出兩條切線的交點Q的坐標(biāo)為 (![]() ,
,![]() )=(
)=(![]() ,﹣2)
,﹣2)
所以 ![]()
![]() (
(![]() ,﹣4)(x2﹣x1,y1﹣y2)
,﹣4)(x2﹣x1,y1﹣y2)
![]() (x22﹣x12)﹣4(
(x22﹣x12)﹣4(![]() x22
x22![]() x12)=0
x12)=0
所以 ![]() 為定值,其值為0.
為定值,其值為0.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)是定義在![]() 上的單調(diào)函數(shù),且對任意的x∈
上的單調(diào)函數(shù),且對任意的x∈![]() 都有
都有![]() ,則方程
,則方程![]() 的一個根所在的區(qū)間是( )
的一個根所在的區(qū)間是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是菱形,四邊形
是菱形,四邊形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為線段
為線段![]() 上的一點.
上的一點.
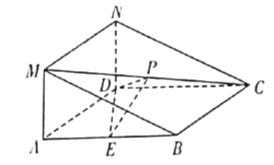
(1)求證:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4―4:坐標(biāo)系與參數(shù)方程]
在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為![]() (θ為參數(shù)),直線l的參數(shù)方程為
(θ為參數(shù)),直線l的參數(shù)方程為![]() .
.
(1)若a=1,求C與l的交點坐標(biāo);
(2)若C上的點到l的距離的最大值為![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)![]() 有下列四個結(jié)論:
有下列四個結(jié)論:
①![]() 是偶函數(shù);②
是偶函數(shù);②![]() 的最小正周期為
的最小正周期為![]() ;③
;③![]() 在
在![]() 上單調(diào)遞增;④
上單調(diào)遞增;④![]() 的值域為
的值域為![]() .
.
上述結(jié)論中,正確的為( )
A.③④B.②④C.①③D.①④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某園林單位準(zhǔn)備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內(nèi)接正方形PQRS為一水池,其余的地方種花.若BC=a,∠ABC=![]() ,設(shè)△ABC的面積為S1,正方形的面積為S2.
,設(shè)△ABC的面積為S1,正方形的面積為S2.
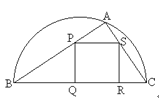
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)當(dāng)a固定,![]() 變化時,求
變化時,求![]() 取最小值時的角
取最小值時的角![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,過點
的焦點,過點![]() 任作兩條互相垂直的直線
任作兩條互相垂直的直線![]() ,
,![]() ,分別交拋物線
,分別交拋物線![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四點,
四點,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
(1)求證:直線![]() 過定點,并求出該定點的坐標(biāo);
過定點,并求出該定點的坐標(biāo);
(2)設(shè)直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,試求
兩點,試求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在
在![]() 處切線與坐標(biāo)軸圍成的三角形面積為
處切線與坐標(biāo)軸圍成的三角形面積為![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)若![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com